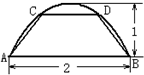
题目内容
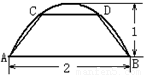
 如图,一块曲线部分是抛物线形的钢板,其底边长为2,高为1,将此钢板切割成等腰梯形的形状,记CD=2x,梯形面积为S.则S的最大值是
如图,一块曲线部分是抛物线形的钢板,其底边长为2,高为1,将此钢板切割成等腰梯形的形状,记CD=2x,梯形面积为S.则S的最大值是| 32 |
| 27 |
| 32 |
| 27 |
分析:建立坐标系,求出抛物线的方程,进而可求梯形的高,从而可求梯形的面积,利用基本不等式即可求得最大值.
解答:解:建立如图所示的坐标系,设抛物线的标准方程为x2=-2py(p>0)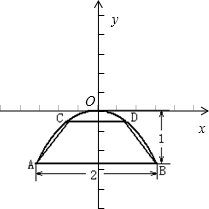
则B(1,-1),代入抛物线方程可得2p=1,∴抛物线方程为x2=-y
∵CD=2x,∴D(x,-x2)
∴梯形的高为1-x2,梯形的面积为S=(x+1)(1-x2),x∈(0,1)
S=(x+1)(1-x2)=
(x+1)2(2-2x)≤
×(
)3=
,
当且仅当x+1=2-2x,即x=
时,S的最大值是
故答案为:

则B(1,-1),代入抛物线方程可得2p=1,∴抛物线方程为x2=-y
∵CD=2x,∴D(x,-x2)
∴梯形的高为1-x2,梯形的面积为S=(x+1)(1-x2),x∈(0,1)
S=(x+1)(1-x2)=
| 1 |
| 2 |
| 1 |
| 2 |
| x+1+x+1+2-2x |
| 3 |
| 32 |
| 27 |
当且仅当x+1=2-2x,即x=
| 1 |
| 3 |
| 32 |
| 27 |
故答案为:
| 32 |
| 27 |
点评:本题考查函数模型的构建,考查抛物线方程,考查函数的最值,确定梯形的高是关键.

练习册系列答案
相关题目
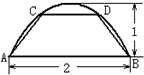 如图,一块曲线部分是抛物线形的钢板,其底边长为2,高为1,将此钢板切割成等腰梯形的形状,记CD=2x,梯形面积为S.则S的最大值是________.
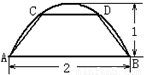
如图,一块曲线部分是抛物线形的钢板,其底边长为2,高为1,将此钢板切割成等腰梯形的形状,记CD=2x,梯形面积为S.则S的最大值是________.