题目内容
奇函数f(x)在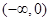
上单调递增，若f(-1)=0,则不等式f(x)<0的解集是( )
A． | B． |
C． | D． |
A
解析考点：奇偶性与单调性的综合．
分析：根据题目条件，画出一个函数图象，再观察即得结果．
解：根据题意，可作出函数图象：
∴不等式f（x）＜0的解集是（-∞，-1）∪（0，1）
故选A．
练习册系列答案
相关题目
已知y=f（x）是定义在R上的增函数，函数y=f（x-1）的图像关于点(1，0)对称，若对于任意的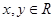
，不等式
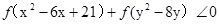恒成立，则当
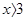时，x2+y2的取值范围是（ ）
| A．（3，7） | B．（9，25） | C．（13，49） | D．（9，49） |
若函数
是定义在R上的偶函数，在
上是减函数，且
则使
的
的取值范围是
A． | B． | C．  | D． |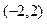
下列函数中，是偶函数的是
A． | B． | C． | D． |
甲乙二人同时从A地赶往B地，甲先骑自行车到中点后改为跑步，而乙则是先跑步，到中点后改为骑自行车，最后二人同时到达B地，甲乙两人骑自行车速度都大于各自跑步速度，又知甲骑自行车比乙骑自行车的速度快。若某人离开A地的距离S与所用时间t的函数用图象表示如下，则在下列给出的四个函数中
|
甲乙二人的图象只可能 （ ）
| A．甲是图①，乙是图② | B．甲是图①，乙是图④ |
| C．甲是图③，乙是图② | D．甲是图③，乙是图④ |
已知函数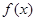
是定义域为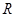
的奇函数，且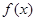的图象关于直线
对称，那么下列式子中对任意
恒成立的是
A． |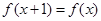
B． |
C． |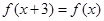
D． |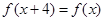
定义在
上的偶函数满足
且
在
上为减函数，若
是锐角三角形的两个内角，则
( )
A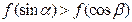． | B． |
C． | D． |
已知函数
是奇函数，当
时，
；当
时，=
A． | B． | C． | D． |
设函数
是R上的奇函数，且当
时，
，
则
等于 （ ）
A． | B． | C．1 | D． |