��Ŀ����
���Ҷ���ͬʱ��A�ظ���B�أ����������г����е���Ϊ�ܲ��������������ܲ������е���Ϊ�����г���������ͬʱ����B�أ��������������г��ٶȶ����ڸ����ܲ��ٶȣ���֪�������г����������г����ٶȿ졣��ij���뿪A�صľ���S������ʱ��t�ĺ�����ͼ���ʾ���£��������и������ĸ�������
|
���Ҷ��˵�ͼ��ֻ���� �� ��
| A������ͼ�٣�����ͼ�� | B������ͼ�٣�����ͼ�� |
| C������ͼ�ۣ�����ͼ�� | D������ͼ�ۣ�����ͼ�� |
B
����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
�溯��f(x)��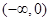 �ϵ�����������f(-1)=0,��ʽf(x)<0�Ľ⼯��( )
�ϵ�����������f(-1)=0,��ʽf(x)<0�Ľ⼯��( )
A�� | B�� |
C�� | D�� |
����  �Ľ����ڵ������ǣ� ��
�Ľ����ڵ������ǣ� ��
| A����0,1�� | B��(1,2) | C��(2,3) | D��(3,4) |
�溯�� �ı���ʽΪ
�ı���ʽΪ �� ��
�� ��
A�� | B�� | C�� | D�� |
��֪ż����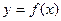 ������
������ ���������������в���ʽһ����������
���������������в���ʽһ����������
A��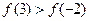 | B��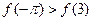 |
C��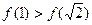 | D��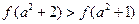 |
����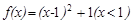 �ķ�����Ϊ��������
�ķ�����Ϊ��������
A�� | B��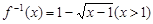 |
C�� | D�� |
�� ����
����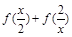 �Ķ�����Ϊ �� ��
�Ķ�����Ϊ �� ��
A��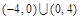 | B�� | C�� | D��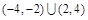 |

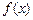 �ķ�����
�ķ����� ��
�� ������
������
 ʱ��f(x)=-x+1�������x�ķ���
ʱ��f(x)=-x+1�������x�ķ��� ����
���� �Ͻ�ĸ����� �� ��
�Ͻ�ĸ����� �� ��