题目内容
若0<a<1,则函数y=loga[1-( )x]在定义域上是
)x]在定义域上是
- A.增函数且y>0
- B.增函数且y<0
- C.减函数且y>0
- D.减函数且y<0
A
分析:本题考查的知识点是指数函数的单调性、对数函数的单调性及复合函数单调性,我们要先求出函数的定义域,然后从内到外逐步分析,( )x、[1-(
)x、[1-( )x]的单调性和取值范围,再结合0<a<1及复合函数“同增异减”的原则,判断loga[1-(
)x]的单调性和取值范围,再结合0<a<1及复合函数“同增异减”的原则,判断loga[1-( )x]的单调性及函数值的取值范围.
)x]的单调性及函数值的取值范围.
解答:要使函数数y=loga[1-( )x]的解析式有意义
)x]的解析式有意义
则1-( )x>0
)x>0
即( )x<1
)x<1
即x>0
当x∈(0,+∞)时,( )x为减函数,且0<(
)x为减函数,且0<( )x<1
)x<1
[1-( )x]为增函数,且0<[1-(
)x]为增函数,且0<[1-( )x]<1
)x]<1
∵0<a<1,故
y=loga[1-( )x]为减函数,且y>0
)x]为减函数,且y>0
故选A
点评:函数y=ax和函数y=logax,在底数a>1时,指数函数和对数函数在其定义域上均为增函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为减函数,而f(-x)与f(x)的图象关于Y轴对称,其单调性相反,故函数y=a-x和函数y=loga(-x),在底数a>1时,指数函数和对数函数在其定义域上均为减函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为增函数.
分析:本题考查的知识点是指数函数的单调性、对数函数的单调性及复合函数单调性,我们要先求出函数的定义域,然后从内到外逐步分析,(
 )x、[1-(
)x、[1-( )x]的单调性和取值范围,再结合0<a<1及复合函数“同增异减”的原则,判断loga[1-(
)x]的单调性和取值范围,再结合0<a<1及复合函数“同增异减”的原则,判断loga[1-( )x]的单调性及函数值的取值范围.
)x]的单调性及函数值的取值范围.解答:要使函数数y=loga[1-(
 )x]的解析式有意义
)x]的解析式有意义则1-(
 )x>0
)x>0即(
 )x<1
)x<1即x>0
当x∈(0,+∞)时,(
 )x为减函数,且0<(
)x为减函数,且0<( )x<1
)x<1[1-(
 )x]为增函数,且0<[1-(
)x]为增函数,且0<[1-( )x]<1
)x]<1∵0<a<1,故
y=loga[1-(
 )x]为减函数,且y>0
)x]为减函数,且y>0故选A
点评:函数y=ax和函数y=logax,在底数a>1时,指数函数和对数函数在其定义域上均为增函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为减函数,而f(-x)与f(x)的图象关于Y轴对称,其单调性相反,故函数y=a-x和函数y=loga(-x),在底数a>1时,指数函数和对数函数在其定义域上均为减函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为增函数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若0<a<1,则函数f(x)=
的图象的大致形状是( )
| xax |
| |x| |
A、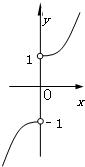 |
B、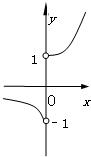 |
C、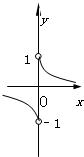 |
D、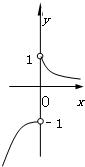 |