题目内容
已知函数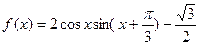 .
.
(1)求函数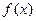 的最小正周期
的最小正周期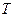 ;
;
(2)若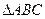 的三边
的三边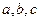 满足
满足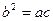 ,且边
,且边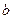 所对角为
所对角为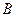 ,试求
,试求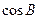 的取值范围,并确定此时
的取值范围,并确定此时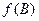 的最大值。
的最大值。
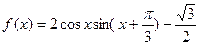 .
.(1)求函数
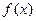 的最小正周期
的最小正周期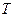 ;
;(2)若
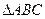 的三边
的三边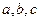 满足
满足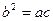 ,且边
,且边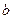 所对角为
所对角为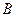 ,试求
,试求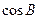 的取值范围,并确定此时
的取值范围,并确定此时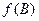 的最大值。
的最大值。解:(1)f(x)=2cosx·sin(x+ )-
)-
=2cosx (sinxcos +cosxsin
+cosxsin )-
)- =2cosx (
=2cosx ( sinx+
sinx+ cosx)-
cosx)-
=sinxcosx+ ·cos2x-
·cos2x- =
= sin2x+
sin2x+ ·
·  -
-
= sin2x+
sin2x+ cos2x=sin (2x+
cos2x=sin (2x+ ).
).
 (2)由余弦定理cosB=
(2)由余弦定理cosB= 得,cosB=
得,cosB= ≥
≥ =
= ,
,
∴ ≤cosB<1,而0<B<π,∴0<B≤
≤cosB<1,而0<B<π,∴0<B≤ .
.
函数f(B)=sin(2B+ ),∵
),∵ <2B+
<2B+ ≤π,当2B+
≤π,当2B+ =
= ,
,
即B= 时,f(B)max=1.
时,f(B)max=1.
 )-
)-
=2cosx (sinxcos
 +cosxsin
+cosxsin )-
)- =2cosx (
=2cosx ( sinx+
sinx+ cosx)-
cosx)-
=sinxcosx+
 ·cos2x-
·cos2x- =
= sin2x+
sin2x+ ·
·  -
-
=
 sin2x+
sin2x+ cos2x=sin (2x+
cos2x=sin (2x+ ).
). (2)由余弦定理cosB=
(2)由余弦定理cosB= 得,cosB=
得,cosB= ≥
≥ =
= ,
,∴
 ≤cosB<1,而0<B<π,∴0<B≤
≤cosB<1,而0<B<π,∴0<B≤ .
.函数f(B)=sin(2B+
 ),∵
),∵ <2B+
<2B+ ≤π,当2B+
≤π,当2B+ =
= ,
,即B=
 时,f(B)max=1.
时,f(B)max=1. 略

练习册系列答案
相关题目
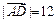 ,
,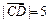 ,
,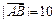 ,
,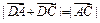 ,
,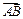 在
在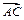 方向上的投影为8;
方向上的投影为8;
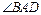 的正弦值;(2)求
的正弦值;(2)求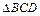 的面积.
的面积.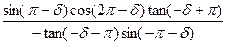
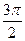 )=
)=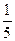 ,求f
,求f (α)的值.
(α)的值.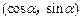 ,
,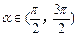 .
.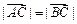 ,求角
,求角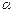 ;
;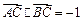 ,求
,求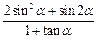 的值.
的值.
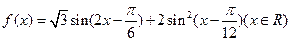
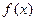 的最小正周期;
的最小正周期; 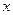 组成的集合.
组成的集合.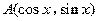 ,其中
,其中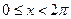 ,
,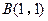 ,
,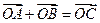 ,
,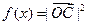 .
.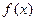 的对称轴和对称中心;
的对称轴和对称中心; .
.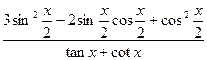 的值.
的值.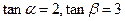 ,则
,则