题目内容
求直线a:2x+y-4=0关于直线l:3x+4y-1=0对称的直线b的方程.
【答案】分析:法一:使用到角公式求所求直线斜率,求得结果;
法二:利用垂直平分来求解对称直线方程.
法三:利用求轨迹方程的方法来求对称直线方程.
解答:解:由
2x+y-4=0,
3x+4y-1=0,
方法一:设直线b的斜率为k,又知直线a的斜率为-2,直线l的斜率为- .
.
则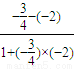 =
=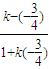 .
.
解得k=-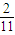 .
.
代入点斜式得直线b的方程为
y-(-2)=-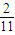 (x-3),
(x-3),
即2x+11y+16=0.
方法二:在直线a:2x+y-4=0上找一点A(2,0),设点A关于直线l的对称点B的坐标为(x,y),
由3×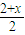 +4×
+4×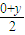 -1=0,
-1=0,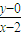 =
= ,
,
解得B(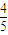 ,-
,-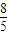 ).
).
由两点式得直线b的方程为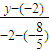 =
=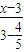 ,
,
即2x+11y+16=0.
方法三:设直线b上的动点P(x,y)关于l:3x+4y-1=0的对称点Q(x,y),则有
3×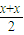 +4×
+4×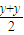 -1=0,
-1=0,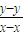 =
= .
.
解得x=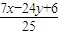 ,y=
,y=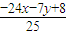 .
.
Q(x,y)在直线a:2x+y-4=0上,
则2×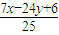 +
+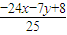 -4=0,
-4=0,
化简得2x+11y+16=0是所求直线b的方程.
点评:本题考查直线关于直线对称问题,三种方法各有优势,本题是基础题.
法二:利用垂直平分来求解对称直线方程.
法三:利用求轨迹方程的方法来求对称直线方程.
解答:解:由
2x+y-4=0,
3x+4y-1=0,
方法一:设直线b的斜率为k,又知直线a的斜率为-2,直线l的斜率为-
 .
.则
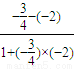 =
=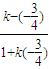 .
.解得k=-
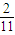 .
.代入点斜式得直线b的方程为
y-(-2)=-
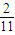 (x-3),
(x-3),即2x+11y+16=0.
方法二:在直线a:2x+y-4=0上找一点A(2,0),设点A关于直线l的对称点B的坐标为(x,y),
由3×
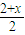 +4×
+4×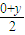 -1=0,
-1=0,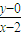 =
= ,
,解得B(
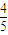 ,-
,-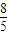 ).
).由两点式得直线b的方程为
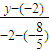 =
=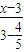 ,
,即2x+11y+16=0.
方法三:设直线b上的动点P(x,y)关于l:3x+4y-1=0的对称点Q(x,y),则有
3×
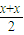 +4×
+4×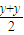 -1=0,
-1=0,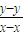 =
= .
.解得x=
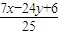 ,y=
,y=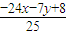 .
.Q(x,y)在直线a:2x+y-4=0上,
则2×
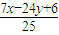 +
+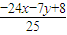 -4=0,
-4=0,化简得2x+11y+16=0是所求直线b的方程.
点评:本题考查直线关于直线对称问题,三种方法各有优势,本题是基础题.

练习册系列答案
相关题目