题目内容
(16分)设{an}是等差数列,其前n项的和为Sn.
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)设{an}各项为正数,a1=![]() ,a1≠a2,若存在互异正整数m,n,p满足:①m+p=2n;
,a1≠a2,若存在互异正整数m,n,p满足:①m+p=2n;
②![]() . 求集合
. 求集合![]() 的元素个数;
的元素个数;
(3)设bn=![]() (a为常数,a>0,a≠1,a1≠a2),数列{bn}前n项和为Tn. 对于正整数c,
(a为常数,a>0,a≠1,a1≠a2),数列{bn}前n项和为Tn. 对于正整数c,
解析:【证】(1){an}为等差数列,设其公差为![]() ,则
,则
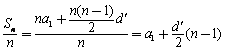 ,于是
,于是![]() (常数),
(常数),
故数列![]() 是等差数列. …………………………3分
是等差数列. …………………………3分
【解】(2)因为{an}为等差数列,所以![]() 是等差数列,
是等差数列,
于是可设![]() 为常数),从而
为常数),从而![]() .
.
因为m+p=2n,所以由![]() 两边平方得
两边平方得
![]() ,即
,即![]() ,
,
亦即![]() ,………………………4分
,………………………4分
于是![]() ,两边平方并整理得
,两边平方并整理得![]() ,即
,即![]() .
.
…………………………6分
因为m≠p,所以![]() ,从而
,从而![]() ,而a1=
,而a1=![]() ,所以
,所以![]() .
.
故![]() . …………………………7分
. …………………………7分
所以![]()
![]() .
.
因为15有4个正约数,所以数对(x,y)的个数为4个.
即集合![]() 中的元素个数为4. ………………………9分
中的元素个数为4. ………………………9分
(3)因为![]() (常数),
(常数),
所以数列{bn}是正项等比数列.
因为a1≠a2,所以等比数列{bn}的公比q≠1. ………………………10分
(解法一)![]() ①
①
![]() . ②
. ②
因为![]() ,所以要证②,只要证
,所以要证②,只要证![]() , ③…………………13分
, ③…………………13分
而③![]()
![]() . ④
. ④
④显然成立,所以③成立,从而有![]() .…………………16分
.…………………16分
(解法二)注意到当n>m时,![]() . ……………………12分
. ……………………12分
于是![]()
![]() . ……………………14分
. ……………………14分
而![]() ,故
,故![]() . ……………………16分
. ……………………16分

练习册系列答案
相关题目
设{an}是等差数列,a1+a3+a5=9,a6=9.则这个数列的前6项和等于( )
| A、12 | B、24 | C、36 | D、48 |