题目内容
若变量a,b满足约束条件 ,n=2a+3b,则n取最小值时,
,n=2a+3b,则n取最小值时, 二项展开式中的常数项为( )
二项展开式中的常数项为( )A.-80
B.80
C.40
D.-20
【答案】分析:画出可行域,求出目标函数n=2a+3b 的最优解,求得n的最小值,在二项展开式通项公式中,令未知数的幂指数等于零,
即可求得常数项.
解答: 解:画出可行域,如图所示:三角形ABC内部区域(包含边界).
解:画出可行域,如图所示:三角形ABC内部区域(包含边界).
目标函数n=2a+3b,A(1,1)为最优解,故n取最小值为5.
 二项展开式通项公式为Tr1=
二项展开式通项公式为Tr1=
 (-1)r x-2r=(-1)r
(-1)r x-2r=(-1)r  25-r
25-r  ,
,
令5-5r=0,可得r=1,故二项展开式中的常数项为-5×24=-80,
故选A.
点评:本题主要考查二项式定理的应用,简单的线性规划问题,体现了数形结合的数学思想,画出图形,是解题的关键,属于中档题.
即可求得常数项.
解答:
 解:画出可行域,如图所示:三角形ABC内部区域(包含边界).
解:画出可行域,如图所示:三角形ABC内部区域(包含边界).目标函数n=2a+3b,A(1,1)为最优解,故n取最小值为5.
 二项展开式通项公式为Tr1=
二项展开式通项公式为Tr1=
 (-1)r x-2r=(-1)r
(-1)r x-2r=(-1)r  25-r
25-r  ,
,令5-5r=0,可得r=1,故二项展开式中的常数项为-5×24=-80,
故选A.
点评:本题主要考查二项式定理的应用,简单的线性规划问题,体现了数形结合的数学思想,画出图形,是解题的关键,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 ,n=2a+3b,则n的最小值为( )
,n=2a+3b,则n的最小值为( )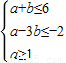 ,n=2a+3b,则n取最小值时,
,n=2a+3b,则n取最小值时,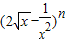 二项展开式中的常数项为( )
二项展开式中的常数项为( )