题目内容
已知a，b，x，y均为正数，且a≠b．
（Ⅰ）求证：（
+
）（x+y）≥（a+b）2，并指出“=”成立的条件；
（Ⅱ）求函数f（x）=
+
（0＜x＜
）的最小值，并指出取最小值时x的值．
（Ⅰ）求证：（
| a2 |
| x |
| b2 |
| y |
（Ⅱ）求函数f（x）=
| 3 |
| x2 |
| 9 |
| 1-3x2 |
| 1 |
| 3 |
（Ⅰ）∵（
+
）（x+y）=a2+
+
+b2=a2+b2+（
+
）
≥a2+b2+2
=a2+b2+ab=（a+b）2，当且仅当ay=bx时取等号．
（II）∵f（x）=
+
=
+
=（
+
）（3x2+1-3x2）
由（I）知，上式≥（3+3）2=36，当且仅当3x2=1-3x2即x2=
时等号成立，
∴函数f（x）=
+
（0＜x＜
）的最小值36，取最小值时x的值为
．
| a2 |
| x |
| b2 |
| y |
| ya2 |
| x |
| xb2 |
| y |
| ya2 |
| x |
| xb2 |
| y |
≥a2+b2+2
|
（II）∵f（x）=
| 3 |
| x2 |
| 9 |
| 1-3x2 |
| 9 |
| 3x2 |
| 9 |
| 1-3x2 |
| 9 |
| 3x2 |
| 9 |
| 1-3x2 |
由（I）知，上式≥（3+3）2=36，当且仅当3x2=1-3x2即x2=
| 1 |
| 6 |
∴函数f（x）=
| 3 |
| x2 |
| 9 |
| 1-3x2 |
| 1 |
| 3 |
| ||
| 6 |
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
＞
，x＞y.
求证：
＞
.
＞
，x＞y.
求证：
＞
.
，x>y，求证：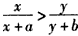
。