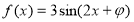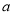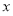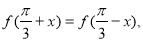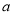题目内容
已知函数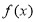 是定义在
是定义在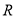 上的奇函数,当
上的奇函数,当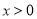 时的解析式为
时的解析式为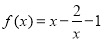 .
.
(Ⅰ)求函数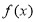 的解析式;
的解析式;
(Ⅱ)求函数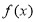 的零点.
的零点.
(Ⅰ) (Ⅱ)零点为
(Ⅱ)零点为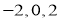
【解析】
试题分析:(Ⅰ) 先利用奇函数的性质求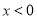 时的解析式,再求
时的解析式,再求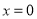 时的解析式,最后写出解析式.
时的解析式,最后写出解析式.
本小题的关键点:(1)如何借助于奇函数的性质求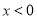 时的解析式;(2)不能漏掉
时的解析式;(2)不能漏掉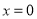 时的解析式.
时的解析式.
(Ⅱ)首先利用求零点的方法:即f(x)=0,然后解方程,同时注意限制范围.
试题解析:(Ⅰ)依题意,函数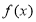 是奇函数,且当
是奇函数,且当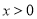 时,
时,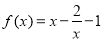 ,
,
 当
当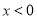 时,
时,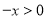 ,
,
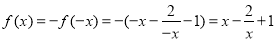 2分
2分
又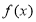 的定义域为
的定义域为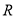 ,
,  当
当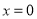 时,
时,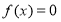 2分
2分
综上可得, 2分
2分
(Ⅱ)当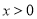 时,令
时,令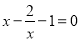 ,即
,即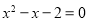 ,解得
,解得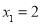 ,
,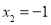 (舍去) 2分
(舍去) 2分
当 时,
时,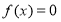 ,
,
 1分
1分
当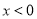 时,令
时,令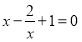 ,即
,即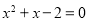 ,解得
,解得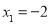 ,
,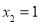 (舍去) 2分
(舍去) 2分
综上可得,函数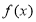 的零点为
的零点为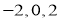 1分
1分
考点:1、奇函数的性质;2、求方程的零点.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目