题目内容
16.已知函数$f(x)=\left\{\begin{array}{l}\frac{2x+1}{x^2},x∈({-∞,-\frac{1}{2}})\\ ln({x+1}),x∈[{-\frac{1}{2},+∞})\end{array}\right.$.g(x)=x2-4x-4.设b为实数,若存在实数a,使f(a)+g(b)=0,则b的取值范围是[-1,5].分析 由分段函数的定义分别求各部分的函数值的取值范围,从而得到函数f(x)的值域,从而化为最值问题即可.
解答 解:当x$∈(-∞,-\frac{1}{2})$时,f(x)=$(\frac{1}{x}+1)^{2}$-1∈[-1,0),
当x$∈[-\frac{1}{2},+∞)$时,f(x)=ln(x+1)∈[-ln2,+∞),
所以f(x)∈[-1,+∞),
所以只要g(b)∈(-∞,1]即可,
即(b-2)2-8∈(-∞,1],
解得b∈[-1,5].
故答案为:[-1,5].
点评 本题考查了分段函数的应用及配方法求最值的应用,同时考查了恒成立问题,属于中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
6.已知数列{an}中,an>0,a1=1,${a_{n+2}}=\frac{1}{{{a_n}+1}}$,a100=a96,则a2016+a3=( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{1+\sqrt{5}}}{2}$ | C. | $\frac{{-1+\sqrt{5}}}{2}$ | D. | $\frac{5}{2}$ |
7.已知等比数列前n项和为Sn,若S2=4,S4=16,则S6=( )
| A. | 52 | B. | 64 | C. | -64 | D. | -52 |
4.已知R是实数集,M=$\{x|\frac{2}{x}<1\},N=\{y|y={x^2}-1\},则({C_R}M)∩N$=( )
| A. | (-1,2) | B. | [一l,2] | C. | (0,2) | D. | [0,2] |
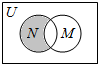 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.