题目内容
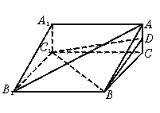
如图,已知A1B1C1—ABC是正三棱柱,D是AC中点.
(Ⅰ)证明:AB1∥平面DBC1;
(Ⅱ)(理)假设AB1⊥BC1,求以BC1为棱的DBC1与CBC1为面的二面角α的度数.
(文)假设AB1⊥BC1,BC=2,求线段AB1在侧面B1BCC1上的射影长.
解析:
如图,(Ⅰ)证明:因为A1B1C1—ABC是三棱柱,所以四边形B1BCC1是矩形,连B1C与BC1交于E,则E为B1C的中点,连DE,D是AC的中点,所以ED∥AB1,又ED (Ⅱ)解:(理)由已知平面ABC⊥平面BB1C1C,在平面ABC内作DF⊥BC,F为垂足,则DF⊥平面B1BCC1,连EF,EF为ED在平面B1BCC1上的射影. 由已知AB1⊥BC1,ED∥AB1,所以ED⊥BC1,由三垂线定理的逆定理知BC1⊥FE,所以∠DEF是二面角D—BC1—C的平面角,设AC=1,则CD= (文)作AF⊥BC,垂足为F.因为面ABC⊥面B1BCC1,所以AF⊥面B1BCC1.连B1F,则B1F是AB1在平面B1BCC1内的射影. ∵BC1⊥AB1 ∴BC1⊥B1F ∵四边形B1BCC1是矩形 ∴∠B1BF=∠BCC1=90°,又∠FB1B=∠C1BC ∴△B1BF∽△BCC1 ∴ 因而B1B2=BF·BC=1×2=2 于是B1F2=B1B2+BF2=3 ∴B1F= 即线段AB1在平面B1BCC1内的射影长为 |

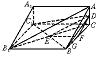
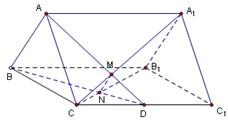 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN. (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.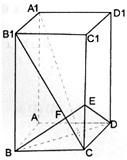 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.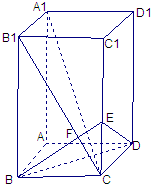 如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F