题目内容
定义在R上的奇函数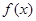 满足:当
满足:当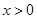 时,
时,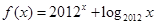 ,则在R上,函数
,则在R上,函数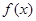 零点的个数为
零点的个数为
3
解析试题分析:显然定义R上的奇函数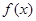 ,必有
,必有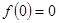 ;作函数
;作函数 、
、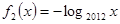 的图像,可发现它们的图像只有一个交点,于是当
的图像,可发现它们的图像只有一个交点,于是当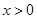 时,
时,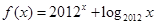 只有一个零点,根据奇函数的对称性可知当
只有一个零点,根据奇函数的对称性可知当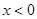 时函数
时函数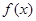 也有一个零点,所以一共有
也有一个零点,所以一共有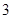 个.
个.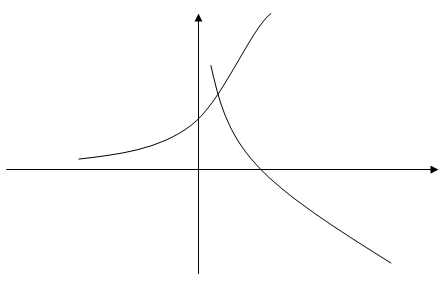
考点:本小题主要考查函数的图像、函数的零点,考查学生的理解、分析能力.

练习册系列答案
相关题目
已知函数 则
则 ( )
( )
A.- | B. | C. | D. |
已知函数 ,若
,若 ,则实数
,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
C.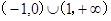 | D. |
已知点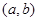 在函数
在函数 的图像上 , 则下列点中不可能在此图像上的是( )
的图像上 , 则下列点中不可能在此图像上的是( )
A. | B. | C. | D. |
已知函数 ,(
,( 且
且 )是
)是 上的减函数,则
上的减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若 ,则( )
,则( )
A. < < < < | B. < < < < |
C. < < < < | D. < < < < |
函数 是幂函数,且在
是幂函数,且在 上为增函数,则实数
上为增函数,则实数 的值是( )
的值是( )
A. | B. | C. | D. 或 或 |
如果函数 的定义域为
的定义域为 ,则实数
,则实数 的值为( )
的值为( )
A.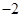 | B. | C. | D. |
 的定义域为
的定义域为 ,若对任意的
,若对任意的 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 上为非减函数,且满足以下三个条件:
上为非减函数,且满足以下三个条件: ;②
;② ;③
;③ .则
.则 ( )
( )


