题目内容
16. 如图△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=45°,且PD=2,BD=6,则AC=5$\sqrt{2}$.
如图△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=45°,且PD=2,BD=6,则AC=5$\sqrt{2}$.
分析 由PDB为圆O的割线,PA为圆的切线,由切割线定理,结合PD=2,BD=6易得PA长,由∠ABC=45°结合弦切角定理,根据PE长求出AE长及ED,DB长,再根据相交弦定理可求出CE,进而得到答案.
解答 解:∵PD=2,BD=6,∴PB=PD+BD=8,
由切割线定理得PA2=PD•PB=16,
∴PA=4,
又∵PE=PA,∴PE=4,
又∠PAC=∠ABC=45°,
∴AE=4$\sqrt{2}$,
又DE=PE-PD=2,BE=BD-DE=4,
由相交弦定理可得:AE•CE=BE•ED=8,
∴CE=$\sqrt{2}$,
∴AC=AE+CE=5$\sqrt{2}$,
故答案:$5\sqrt{2}$.
点评 本题考查的知识点是与圆相关的比例线段,根据已知条件求出与圆相关线段的长,构造方程组,求出未知线段是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.正方体的棱长为1,C、D、M分别为三条棱的中点,A、B是顶点,那么点M到截面ABCD的距离是( ) 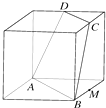

| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
8.已知函数f(x)=$\left\{\begin{array}{l}{x+2,x>a}\\{{x}^{2}+5x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是( )
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |
 如图,将边长为2的正方形ABCD沿对角线BD对折,使得平面BCD⊥平面ABD,点E是BD中点,点F满足:FA∥CE,且FA=2$\sqrt{2}$.
如图,将边长为2的正方形ABCD沿对角线BD对折,使得平面BCD⊥平面ABD,点E是BD中点,点F满足:FA∥CE,且FA=2$\sqrt{2}$.