题目内容
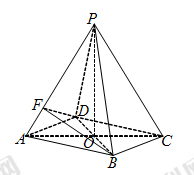
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且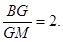
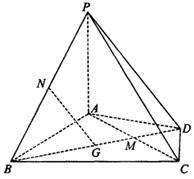
(Ⅰ)求证:AB⊥PD;
(Ⅱ)求证:GN//平面PCD.
(Ⅰ)证明:见解析;(Ⅱ)见解析.
解析试题分析:(Ⅰ)利用 平面
平面 ,得到
,得到 ,再由
,再由  ,即证得
,即证得  平面
平面 .由
.由  平面
平面 得证.
得证.
(Ⅱ)根据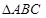 是正三角形,且
是正三角形,且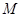 是
是 中点,
中点,
可得 .
.
在直角三角形 中,可得
中,可得  ,
,
在直角三角形 中,可得
中,可得 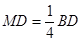 ,再根据
,再根据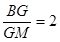 ,得到
,得到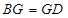 ,而
,而 为线段
为线段 的中点, 得到
的中点, 得到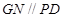 即可推出
即可推出 平面
平面 .
.
试题解析:(Ⅰ)证明:因为 平面
平面 ,所以
,所以 , 2分
, 2分
又因为 ,所以
,所以 平面
平面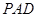 , 4分
, 4分
又 平面
平面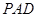 ,所以
,所以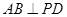 . 6分
. 6分
(Ⅱ)因为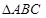 是正三角形,且
是正三角形,且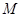 是
是 中点,
中点,
所以 , 7分
, 7分
在直角三角形 中,
中, ,所以
,所以 ,
,
在直角三角形 中,
中, ,
,
所以 ,所以
,所以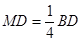 , 10分
, 10分
又因为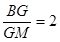 ,所以
,所以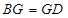 ,又
,又 为线段
为线段 的中点,所以
的中点,所以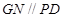 ,
, 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 12分
12分
考点:平行关系,垂直关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,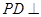 面
面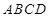 ,
,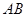 ∥
∥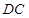 ,
,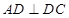 ,
,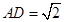 ,
,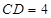 ,
,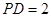 ,
, 为
为 上一点,
上一点,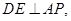
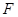 是平面
是平面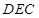 与
与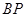 的交点.
的交点.
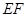 ∥
∥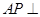 面
面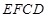 ;
; 与面
与面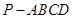 中,底面
中,底面 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且 交
交 于点
于点 .
.
 ;
; .
. 的侧棱长和底面边长均为2,
的侧棱长和底面边长均为2, 在底面ABC内的射影O为底面△ABC的中心,如图所示:
在底面ABC内的射影O为底面△ABC的中心,如图所示:
 ,求异面直线
,求异面直线 与
与 、
、 ,求三棱锥C1-BCA1的体积.
,求三棱锥C1-BCA1的体积. 的直角边
的直角边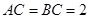 ,沿其中位线
,沿其中位线 将平面
将平面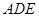 折起,使平面
折起,使平面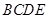 ,得到四棱锥
,得到四棱锥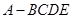 ,设
,设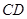 、
、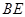 、
、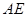 、
、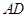 的中点分别为
的中点分别为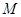 、
、 、
、 、
、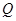 .
.


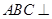 平面
平面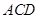 ;
;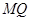 所成的角.
所成的角.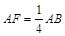 .
.
 中,底面四边形
中,底面四边形 是菱形,
是菱形, ,
, 是边长为2的等边三角形,
是边长为2的等边三角形, ,
,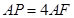 .
.
 底面
底面 与平面
与平面 所成角的大小;
所成角的大小; 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面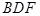 ?如果存在,求
?如果存在,求 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
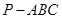 中,
中, 平面
平面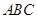 ,
,
 ,
, ,
,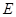 为
为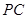 中点.
中点.
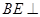 平面
平面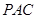 ;
; 的正弦值.
的正弦值.