题目内容
如图,已知椭圆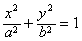 (a> b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A、B。
(a> b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A、B。
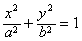 (a> b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A、B。
(a> b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A、B。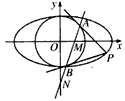
(1)①若圆O过椭圆的两个焦点,求椭圆的离心率e;
②若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e 的取值范围;
(2)设直线AB与x轴、y轴分别交于点M、N,求证: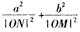 为定值。
为定值。
②若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e 的取值范围;
(2)设直线AB与x轴、y轴分别交于点M、N,求证:
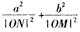 为定值。
为定值。解:(1)①∵圆O过椭圆的焦点,圆O:x2+y2=b2,
∴b=c,
∴b2=a2-c2=c2,
∴a2=2c2,
∴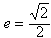 ;
;
②由∠APB=90°及圆的性质,知四边形OBPA为正方形,可得

∴|OP|2=2b2≤a2,
∴a2≤2c2
∴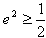 ,
, 。
。
(2)设P(x0,y0),A(x1,y1),B(x2,y2),
则切线PA方程为:x1x+y1y=b2,PB方程为:x2x+y2y=b2
∴x1x+y1y=x2x+y2y,
∴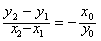
直线AB方程为: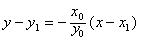
即x0x+y0y=b2
令x=0,得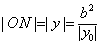
令y=0得
∴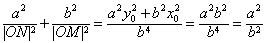
∴ 为定值,定值是
为定值,定值是 。
。
∴b=c,
∴b2=a2-c2=c2,
∴a2=2c2,
∴
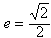 ;
;②由∠APB=90°及圆的性质,知四边形OBPA为正方形,可得

∴|OP|2=2b2≤a2,
∴a2≤2c2
∴
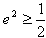 ,
, 。
。(2)设P(x0,y0),A(x1,y1),B(x2,y2),
则切线PA方程为:x1x+y1y=b2,PB方程为:x2x+y2y=b2
∴x1x+y1y=x2x+y2y,
∴
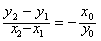
直线AB方程为:
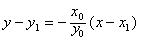
即x0x+y0y=b2
令x=0,得
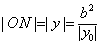
令y=0得

∴
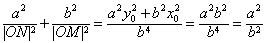
∴
 为定值,定值是
为定值,定值是 。
。
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过顶点A、B的直线与原点的距离为
,过顶点A、B的直线与原点的距离为 .
.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点
,过点 和
和 的直线与原点的距离为
的直线与原点的距离为 .
. ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两点.问:是否存在
两点.问:是否存在 的值,使以
的值,使以 为直径的圆过
为直径的圆过 点?请说明理由.
点?请说明理由.