题目内容
数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an= .
2^(n+1)-3
解:∵数列{an}中,a1=1,an=2an-1+3,
∴an+3=2(an-1+3)(n≥2),
∴{an+3}是公比为2,首项为4的等比数列,
∴an+3=4•2n-1,
∴an=2n+1-3.
故答案为:2n+1-3.
∴an+3=2(an-1+3)(n≥2),
∴{an+3}是公比为2,首项为4的等比数列,
∴an+3=4•2n-1,
∴an=2n+1-3.
故答案为:2n+1-3.

练习册系列答案
相关题目
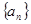 中,
中,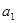 和
和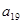 为方程
为方程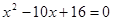 的两根,则
的两根,则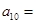 ( )
( )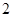

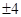
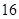
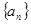 中, 若
中, 若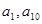 是方程
是方程 的两根,则
的两根,则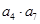 = .
= .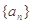 是等比数列,且公比
是等比数列,且公比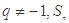 是
是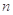 项和,已知
项和,已知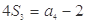 ,
,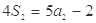 ,则公比
,则公比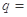 ( )
( )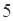



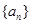 的前
的前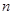 项和记为
项和记为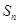 ,若
,若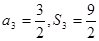 ,求求通项
,求求通项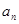 .
.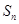 为等比数列
为等比数列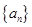 的前
的前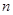 项和,已知
项和,已知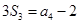 ,
,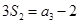 ,则公比
,则公比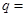 ( )
( )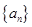 中,
中,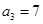 ,前3项之和
,前3项之和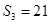 ,则公比
,则公比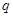 的值为 ( )
的值为 ( )
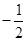
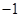 或
或
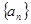 中,若
中,若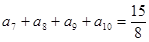 ,
,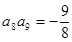 ,则
,则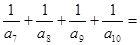 ____________
____________