题目内容
(本小题满分14分)
已知向量 、
、 、
、 两两所成的角相等,并且|
两两所成的角相等,并且| |=1,|
|=1,| |=2,|
|=2,| |=3.
|=3.
(Ⅰ)求向量 +
+ +
+ 的长度;
的长度;
(Ⅱ)求 +
+ +
+ 与
与 的夹角.
的夹角.
已知向量
 、
、 、
、 两两所成的角相等,并且|
两两所成的角相等,并且| |=1,|
|=1,| |=2,|
|=2,| |=3.
|=3.(Ⅰ)求向量
 +
+ +
+ 的长度;
的长度;(Ⅱ)求
 +
+ +
+ 与
与 的夹角.
的夹角.(Ⅰ)| +
+ +
+ |=
|=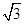 .(Ⅱ)
.(Ⅱ) 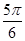 .
.
 +
+ +
+ |=
|=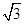 .(Ⅱ)
.(Ⅱ) 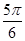 .
.试题分析:(Ⅰ)设向量
 、
、 、
、 两两所成的角均为
两两所成的角均为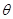 ,则
,则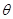 =0或
=0或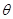 =
=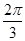 , 又|
, 又| |=1,|
|=1,| |=2,|
|=2,| |=3.则当
|=3.则当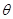 =0时,
=0时, ·
· =|
=| |·|
|·| |
|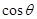 =2,
=2, ·
· =|
=| |·|
|·| |
|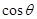 =6,
=6, ·
· =|
=| |·|
|·| |
|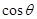 =3,此时 |
=3,此时 | +
+ +
+ |2=
|2= 2+
2+ 2+
2+ 2+2
2+2 ·
· +2
+2 ·
· +2
+2 ·
· =14+22=36,∴ |
=14+22=36,∴ | +
+ +
+ |=6;
|=6;当
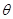 =
=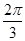 时,
时, ·
· =|
=| |·|
|·| |
|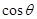 =-1,
=-1, ·
· =|
=| |·|
|·| |
|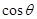 =-3,
=-3, ·
· =|
=| |·|
|·| |
|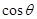 =-
=-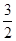 ,此时 |
,此时 | +
+ +
+ |2=
|2= 2+
2+ 2+
2+ 2+2
2+2 ·
· +2
+2 ·
· +2
+2 ·
· =14-11=3,∴ |
=14-11=3,∴ | +
+ +
+ |=
|=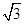 .
.(Ⅱ)当
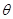 =0,即|
=0,即| +
+ +
+ |=6时,
|=6时, +
+ +
+ 与
与 的夹角显然为0; 当
的夹角显然为0; 当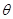 =
=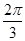 ,即|
,即| +
+ +
+ |=
|=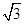 时,∵ (
时,∵ ( +
+ +
+ )·
)· =-
=-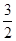 ,且|
,且| +
+ +
+ |·|
|·| |=
|=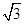 ,
,  <
< +
+ +
+ ,
, >=-
>=-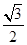 ,∴
,∴ +
+ +
+ 与
与 的夹角为
的夹角为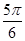 .
.点评:熟练运用向量的运算及数量积的概念是解决此类求模和夹角的常用方法

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 //
//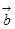 ,
,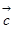 ,则
,则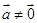 ,
,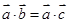 ,则
,则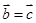 ;
;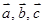 都有
都有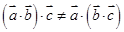 ;
; 使得
使得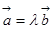 ,则向量
,则向量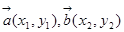 ,若
,若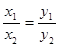 其中正确的是
其中正确的是 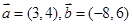 ,则
,则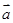 与
与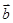 ( )
( )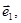
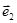 是同一平面内两个不共线的向量,且
是同一平面内两个不共线的向量,且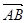 =2
=2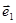 +k
+k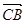 =
=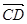 =2
=2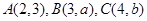 共线,则有( )
共线,则有( )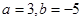
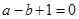
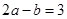
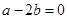
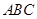 中,
中,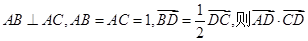 的值等于 .
的值等于 .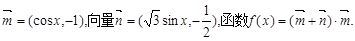
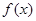 的最小正周期T;
的最小正周期T;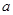 ,b,c分别为△ABC内角A,B,C的对边,A为锐角,
,b,c分别为△ABC内角A,B,C的对边,A为锐角,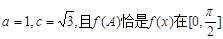 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积.
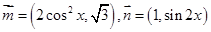 ,函数
,函数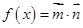
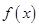 的单调增区间;
的单调增区间;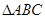 中,
中,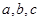 分别是角A, B, C的对边,且
分别是角A, B, C的对边,且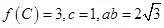 ,且
,且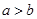
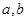 的值.
的值.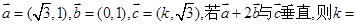 ( )
( )