题目内容
已知向量 ,
,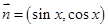 ,设函数
,设函数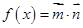 .
.
(Ⅰ)求函数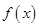 的解析式,并求
的解析式,并求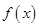 在区间
在区间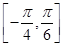 上的最小值;
上的最小值;
(Ⅱ)在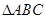 中,
中,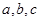 分别是角
分别是角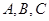 的对边,
的对边,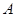 为锐角,若
为锐角,若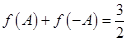 ,
, 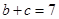 ,
,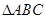 的面积为
的面积为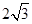 ,求
,求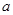 .
.
 ,
,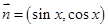 ,设函数
,设函数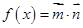 .
.(Ⅰ)求函数
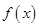 的解析式,并求
的解析式,并求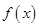 在区间
在区间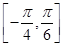 上的最小值;
上的最小值;(Ⅱ)在
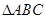 中,
中,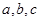 分别是角
分别是角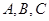 的对边,
的对边,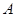 为锐角,若
为锐角,若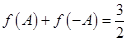 ,
, 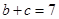 ,
,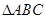 的面积为
的面积为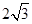 ,求
,求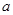 .
.(1)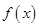 =
= ,
,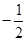 (2)
(2)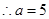
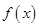 =
= ,
,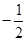 (2)
(2)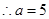
试题分析:解:(Ⅰ)
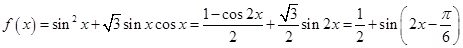 3分
3分因为
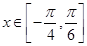 ,所以
,所以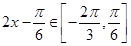 .
.所以当
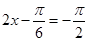 时,函数
时,函数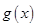 在区间
在区间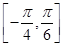 上的最小值为
上的最小值为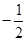 . 6分
. 6分(Ⅱ)由
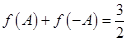 得:
得: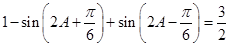 .
.化简得:
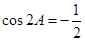 ,又因为
,又因为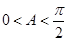 ,解得:
,解得: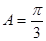 . 9分
. 9分由题意知:
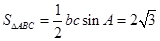 ,解得
,解得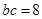 ,又
,又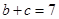 ,
,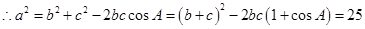 ,
,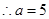 . 12分
. 12分点评:主要是考查了三角函数中二倍角公式以及正弦定理和余弦定理的运用,属于中档题。

练习册系列答案
相关题目
 中,
中, ,则角
,则角 _____________。
_____________。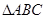 中,
中,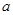 、
、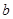 、
、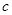 分别是角
分别是角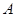 、
、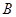 、
、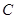 的对边,
的对边,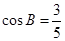 ,且符合
,且符合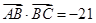 .
.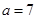 ,求角
,求角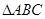 中,
中,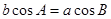 ,则三角形的形状为( )
,则三角形的形状为( )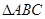 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为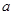 、
、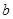 、
、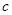 ,且
,且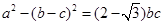 ,
,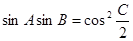 ,
,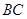 边上中线
边上中线 的长为
的长为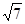 .
.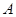 和角
和角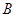 的大小;
的大小;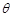 ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2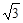 m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4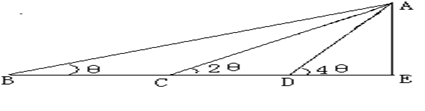
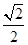 、
、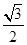 、
、 ,则三棱锥A—BCD的外接球的体积为 ( )
,则三棱锥A—BCD的外接球的体积为 ( )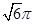 B.2
B.2 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,求△
,求△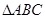 中,内角
中,内角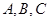 所对的分别是
所对的分别是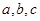 ,已知
,已知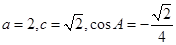 ;
;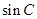 和
和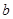 的值; (II)求
的值; (II)求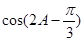 的值.
的值.