题目内容
已知p:函数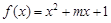 有两个零点,q:
有两个零点,q: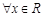 ,
,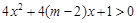 .若若
.若若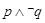 为真,则实数m的取值范围为
为真,则实数m的取值范围为
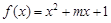 有两个零点,q:
有两个零点,q: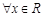 ,
,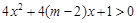 .若若
.若若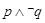 为真,则实数m的取值范围为
为真,则实数m的取值范围为A.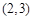 | B.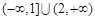 | C.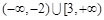 | D.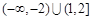 |
C
由p∧¬q为真,知p是真命题,q是假命题,由p得△=m2-4>0,解得m>2或m<-2.由¬q,得△=16(m-2)2-16≥0,解得m≥3或m≤1,由此能求出实数m的取值范围.
解答:解:∵p∧¬q为真,
∴p是真命题,q是假命题,
由p:函数f(x)=x2+mx+1有两个零点,
得△=m2-4>0,解得m>2或m<-2.
由¬q:存在x∈R,4x2+4(m-2)x+1≤0,
得△=16(m-2)2-16≥0,
解得m≥3或m≤1,
∴实数m的取值范围为(-∞,-2)∪[3,+∞).
故选C.
解答:解:∵p∧¬q为真,
∴p是真命题,q是假命题,
由p:函数f(x)=x2+mx+1有两个零点,
得△=m2-4>0,解得m>2或m<-2.
由¬q:存在x∈R,4x2+4(m-2)x+1≤0,
得△=16(m-2)2-16≥0,
解得m≥3或m≤1,
∴实数m的取值范围为(-∞,-2)∪[3,+∞).
故选C.

练习册系列答案
相关题目
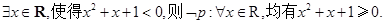
 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件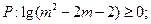 若命题
若命题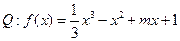 在
在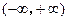 内单调递增,如果“
内单调递增,如果“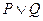 ”
”  为真命题,“
为真命题,“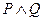 ”为假命题,求实数
”为假命题,求实数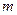 的取值范围。
的取值范围。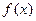 ,有下述命题:
,有下述命题: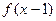 的图象关于点A(1,0)对称
的图象关于点A(1,0)对称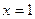
 对称,则
对称,则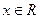 ,有
,有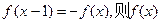 的周期为2
的周期为2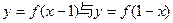 的图象关于直线
的图象关于直线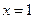 对称.
对称.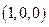 的距离小于或等于1的点集合为( )
的距离小于或等于1的点集合为( )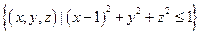
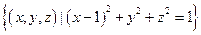
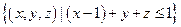
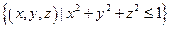
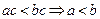
 ;
;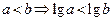 ;
;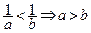 ;
;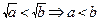 ;
; P:"所有的x∈R, sinx≥1"的否定是( )
P:"所有的x∈R, sinx≥1"的否定是( )