题目内容
如果关于x的一元二次方程x2-2（a-3）x-b2+9=0中，a、b分别是两次投掷骰子所得的点数，则该二次方程有两个正根的概率P=（ ）A．
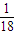
B．
C．
D．
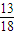
【答案】分析：这是一个古典概型问题，总件数由分步计数原理知是36，满足条件的事件数在整理时要借助于根与系数之间的关系，根的判别式，要进行讨论得到结果．
解答：解：方程的两根要大于0，由韦达定理得 2（a-3）＞0，-b2+9＞0 解得a＞3，b＜3 若b=2，9-b2=5 要使方程有两个正根，判别式=4（a-3）2-4×5＞0 （a-3）2＞5，解得，a=6 若b=1，9-b2=8 判别式=4（a-3）2-4×8＞0 （a-3）2＞8，解得，a=6 a，b只有两种情况满足要求：a=6，b=1，2 而投掷骰子所产生的a，b的总的可能组合有：6×6=36 所以有两个正根的概率是：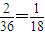
，
故选A
点评：解决古典概型问题时，先要判断该概率模型是不是古典概型，再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数．
解答：解：方程的两根要大于0，由韦达定理得 2（a-3）＞0，-b2+9＞0 解得a＞3，b＜3 若b=2，9-b2=5 要使方程有两个正根，判别式=4（a-3）2-4×5＞0 （a-3）2＞5，解得，a=6 若b=1，9-b2=8 判别式=4（a-3）2-4×8＞0 （a-3）2＞8，解得，a=6 a，b只有两种情况满足要求：a=6，b=1，2 而投掷骰子所产生的a，b的总的可能组合有：6×6=36 所以有两个正根的概率是：
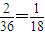，故选A
点评：解决古典概型问题时，先要判断该概率模型是不是古典概型，再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数．
练习册系列答案
阅读快车系列答案
相关题目
，x1•x2＝
．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：
＝
＝
＝
．