题目内容
设实数x，y满足3≤xy2≤8，4≤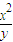
≤9，则
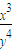的最大值是 ．
【答案】分析：首先分析题目由实数x，y满足条件3≤xy2≤8，4≤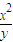
≤9．求
的最大值的问题．根据不等式的等价转换思想可得到：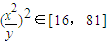
，
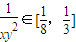，代入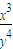
求解最大值即可得到答案．
解答：解：因为实数x，y满足3≤xy2≤8，4≤
≤9，
则有：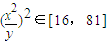
，
，
又
，
即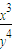
的最大值是27．
故答案为27．
点评：此题主要考查不等式的基本性质和等价转化思想，等价转换思想在考试中应用不是很广泛，但是对于特殊题目能使解答更简便，也需要注意．
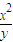≤9．求的最大值的问题．根据不等式的等价转换思想可得到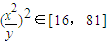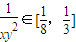：，，代入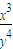求解最大值即可得到答案．解答：解：因为实数x，y满足3≤xy2≤8，4≤
≤9，则有：
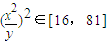，，又
，即
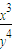的最大值是27．故答案为27．
点评：此题主要考查不等式的基本性质和等价转化思想，等价转换思想在考试中应用不是很广泛，但是对于特殊题目能使解答更简便，也需要注意．
练习册系列答案
相关题目
≤9，则
的最大值是 ．