题目内容
已知直角坐标平面中有两个定点M(-1,0)、N(1,0),问在此平面内是否存在一点P,使得下面两个条件:
(1)P到M的距离与P到点N距离的比为
(2)点N到直线PM的距离为
同时成立?若存在,请求出P点坐标;若不存在,请说明理由.
(1)P到M的距离与P到点N距离的比为
| 2 |
(2)点N到直线PM的距离为
| 2 |
分析:(1)设P(x,y),由(1)的条件P到点M(-1,0)距离与到点N(1,0)距离的比为
,利用两点间的距离公式可得
=
,
=
,化简即可得到一个方程;
(2)令lPM:y=k(x+1),kx-y+k=0可得点N到直线PM的距离d=
=
,即可解得k.与(1)圆的方程联立即可解得.
| 2 |
| |PM| |
| |PN| |
| 2 |
| ||
|
| 2 |
(2)令lPM:y=k(x+1),kx-y+k=0可得点N到直线PM的距离d=
| |2k| | ||
|
| 2 |
解答:解:(1)设P(x,y),因P到点M(-1,0)距离与到点N(1,0)距离的比为
.
即
=
,
=
,
化简得:x2-6x+y2+1=0.
(2)令lPM:y=k(x+1),kx-y+k=0
点N到直线PM的距离d=
=
,k=±1.
∴直线PM方程是y=±(x+1).
由
得:x2-2x+1=0,解得x=1.
代入得y2=4,解得y=±2.
∴P(1,±2).
所以存在这样的P点(1,2)、(1,-2)使条件(1)(2)同时成立.
| 2 |
即
| |PM| |
| |PN| |
| 2 |
| ||
|
| 2 |
化简得:x2-6x+y2+1=0.
(2)令lPM:y=k(x+1),kx-y+k=0
点N到直线PM的距离d=
| |2k| | ||
|
| 2 |
∴直线PM方程是y=±(x+1).
由
|
代入得y2=4,解得y=±2.
∴P(1,±2).
所以存在这样的P点(1,2)、(1,-2)使条件(1)(2)同时成立.
点评:熟练掌握两点间的距离公式、点到直线的距离公式、直线与圆的位置关系等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
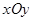 中,
中,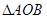 三个顶点的直角坐标分别为
三个顶点的直角坐标分别为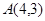 ,
,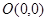 ,
,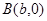 .
.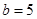 ,求
,求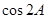 的值;
的值;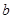 的取值范围.
的取值范围.