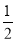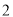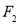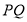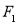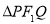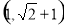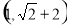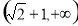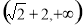题目内容
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
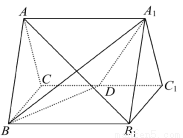
(1)求证:直线AB1⊥平面A1BD.
(2)求二面角A-A1D-B正弦值的大小.
(1)证明过程详见试题解析;(2)二面角A-A1D-B正弦值为 .
.
【解析】
试题分析:(1)建立如下图的空间坐标系,要证直线AB1⊥平面A1BD,只需证明
即可.(2)先求出平面A1AD的一个法向量 ,再用向量夹角公式求二面角A-A1D-B正弦值.
,再用向量夹角公式求二面角A-A1D-B正弦值.
试题解析:(1)取BC中点O,连接AO,
∵△ABC为正三角形,∴AO⊥BC,
∵直棱柱ABC-A1B1C1,∴平面ABC⊥平面BCC1B1且相交于BC,
∴AO⊥平面BCC1B1.取B1C1中点O1,则OO1∥BB1,∴OO1⊥BC.
以O为原点,如图建立空间直角坐标系O-xyz,
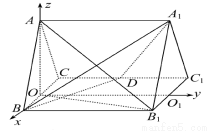
则B(1,0,0),D(-1,1,0),A1(0,2, )A(0,0,
)A(0,0, ),B1(1,2,0),C(-1,0,0),
),B1(1,2,0),C(-1,0,0),
∴

∴直线AB1⊥平面A1BD. 6分
(2)设平面A1AD的一个法向量为
n=(x,y,z).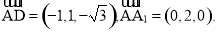
∵
∴ 令z=1得n=(-
令z=1得n=(- ,0,1)为平面A1AD的一个法向量.
,0,1)为平面A1AD的一个法向量.
由(1)知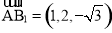 为平面A1BD的法向量.
为平面A1BD的法向量.
∴
∴二面角A-A1D-B正弦值的大小为 . 12分
. 12分
考点:空间向量、直线与平面的位置关系.

假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 1.4 | 2.3 | 3.1 | 3.7 | 4.5 |
若由资料可知y对x呈线性相关关系,且线性回归方程为=a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为________.
对具有线性相关关系的变量 ,
, 测得一组数据如下表:
测得一组数据如下表:
x | 2 | 4 | 5 | 6 | 8 |
y | 20 | 40 | 60 | 80 | 100 |
根据上表,利用最小二乘法得到它们的回归直线方程为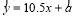 .据此模型预测
.据此模型预测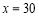 时,
时, 的估计值为( )
的估计值为( )
A. 320 B. 320.5 C. 322.5 D. 321.5