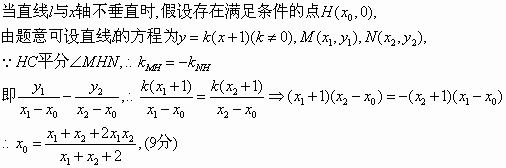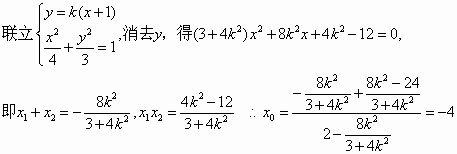题目内容
已知定圆A：
，圆心为A，动圆M过点B(1，0)，且和圆A相切，动圆的圆心M的轨迹记为C．
(1)求曲线C的方程；
(2)过点C(－1，0)任作一条与y轴不垂直的直线交曲线于M、N两点，在x轴上是否存在点H，使HC平分∠MHN？若存在，求出点H的坐标，若不存在，请说明理由．
答案：
解析：
解析：
|
解：(1)圆A的圆心为 故 (2)当 |
，设动圆M的圆心M(x，y)，半径为
，依题意有，
＝|MB|．
，可知点B在圆A内，从而圆M切于圆A，
，∴点M的轨迹是以A、B为焦点的椭圆，设椭圆
故曲线C的方程为
练习册系列答案
相关题目