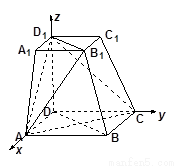题目内容
用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台。
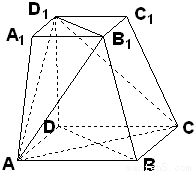
如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2,
(Ⅰ)求证:B1B∥平面D1AC;
(Ⅱ)求平面B1AD1与平面CAD1夹角的余弦值。
如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2,
(Ⅰ)求证:B1B∥平面D1AC;
(Ⅱ)求平面B1AD1与平面CAD1夹角的余弦值。

| 解:以D为原点,以DA、DC、DD1所在直线 分别为x轴,y轴,z轴 建立空间直角坐标系D-xyz, 如图,则有A(2,0,0), B(2,2,0),C(0,2,0), A1(1,0,2),B1(1,1,2), C1(0,1,2),D1(0,0,2), (Ⅰ)证明:设 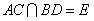 ,连接D1、E, ,连接D1、E,则有  , ,所以  , ,∵  , ,∴ 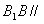 平面 平面 ; ;(Ⅱ) 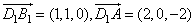 , ,设  为平面AB1D1的法向量, 为平面AB1D1的法向量, , ,于是令x=1,则y=-1,z=1, 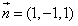 , ,同理可以求得平面  的一个法向量 的一个法向量 , , , ,∴二面角  的余弦值为 的余弦值为 。 。 |
 |

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
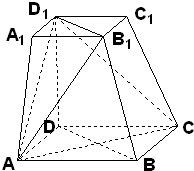 用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2. 中,下底
中,下底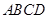 是边长为
是边长为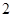 的正方形,上底
的正方形,上底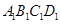 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱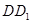 ⊥平面
⊥平面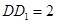 .
.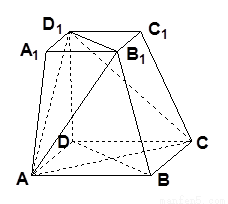
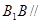 平面
平面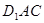 ;
;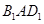 与平面
与平面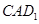 夹角的余弦值.
夹角的余弦值.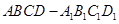 中,下底
中,下底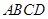 是边长为
是边长为 的正方形,上底
的正方形,上底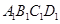 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 ⊥平面
⊥平面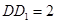 .
.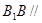 平面
平面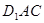 ;
;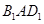 与平面
与平面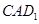 夹角的余弦值.
夹角的余弦值.