题目内容
在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式如从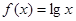 可抽象出
可抽象出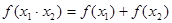 的性质,那么由
的性质,那么由 = (填一个具体的函数)可抽象出性质
= (填一个具体的函数)可抽象出性质
【答案】
任意指数函数均可,如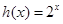
【解析】略

练习册系列答案
相关题目
题目内容
在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式如从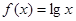 可抽象出
可抽象出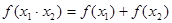 的性质,那么由
的性质,那么由 = (填一个具体的函数)可抽象出性质
= (填一个具体的函数)可抽象出性质
任意指数函数均可,如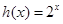
【解析】略
