题目内容

若关于x的方程
|1-x2|
+kx=
2
有3个不等实数根，则实数k的取值范围为
 
．
分析：构造函数y1=
|1-x2|
，y2=-kx+
2
，做出图象，求出相应方程只有一根情形，即可得出结论．
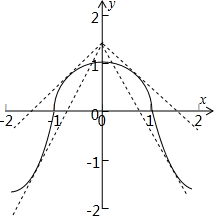解答：精英家教网解：构造函数y1=
|1-x2|
，y2=-kx+
2
，图象如图所示．
由
1-x2
=-kx+
2
，可得(k2+1)x2-2
2
kx+1=0，由△=0，可得k=±
2
；
由
x2-1
=-kx+
2
，可得(k2-1)x2-2
2
kx+3=0，当k=±1时，方程只有一个根，
∴关于x的方程
|1-x2|
+kx=
2
有3个不等实数根，实数k的取值范围为(-
2
，-1)∪(1，
2
)．
故答案为：(-
2
，-1)∪(1，
2
)．
点评：本题考查函数的零点与方程根的关系，考查数形结合的数学思想，考查学生的计算能力，正确作出函数的图象是关键．
练习册系列答案
相关题目
若关于x的方程
.
1-x2+2x
3-a
.
=0有解，则实数a的取值范围是
 
．
若关于x的方程
1-x2
=k(x-2)有两个不相等的实根，则实数K的取值范围是（　　）
A、(-
3
，
3
)
B、(-
3
3
，
3
3
)
C、(-
3
3
，0]
D、(-
3
3
，-
1
2
]∪[
1
2
，
3
3
)
已知函数f（x）=
1-x
ax
+lnx（x＞0）．
（1）当a=1时，求f（x）在[
1
2
，2]上的最小值；
（2）若函数f（x）在[
1
2
，+∞）上为增函数，求正实数a的取值范围；
（3）若关于x的方程1-x+2xlnx-2mx=0在区间[
1
e
，e]内恰有两个相异的实根，求实数m的取值范围．
若关于x的方程
1-x2
=kx+2恰有两个实根，则k的取值范围是
[-2，-
3
)∪(
3
，2]
[-2，-
3
)∪(
3
，2]
．
已知函数f(x)=
3
asinωx•cosωx-cos2ωx+
3
2
(ω∈R+，a∈R)的最小正周期为π，其图象关于直线x=
π
6
对称．
（1）求函数f（x）在[0，
π
2
]上的单调递增区间；
（2）若关于x的方程1-f（x）=m在[0，
π
2
]上只有一个实数解，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网