题目内容
函数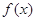 的定义域为
的定义域为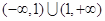 ,且
,且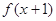 为奇函数,当
为奇函数,当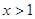 时,
时, ,则直线
,则直线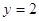 与函数
与函数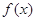 图象的所有交点的横坐标之和是( )
图象的所有交点的横坐标之和是( )
| A.1 | B.2 | C.4 | D.5 |
D
解析考点:奇偶性与单调性的综合.
分析:f(x+1)为奇函数可得函数f(x)的图象关于(1,0)对称,从而可求x<1时的函数解析式,进而解方程f(x)=2可得.
解:f(x+1)为奇函数,函数图象关于(0,0)对称
函数f(x)的图象关于(1,0)对称
当x>1时,f(x)=2x2-12x+16
当x<1时,f(x)=-2x2-4x
令2x2-12x+16=2可得x1+x2=6
令-2x2-4x=2可得x3=-1
横坐标之和为5
故选D

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,且
,且 为
为 的导函数,函数
的导函数,函数 的图象如图所示.则不等式组
的图象如图所示.则不等式组 所表示的平面区域的面积是
所表示的平面区域的面积是
A.3 | B.4 | C.5 | D. |
 的定义域为
的定义域为 ,且
,且 为偶函数,则实数
为偶函数,则实数 的值可以是
的值可以是 B.
B. C.
C. D.
D.
 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数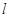 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的
上的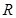 的函数
的函数 时,
时, ,且
,且 的取值范围是
的取值范围是  . B.
. B. 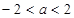
 D.
D.
 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数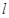 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的
上的 的函数
的函数 时,
时, ,且
,且 的取值范围是
的取值范围是
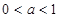 . B.
. B. 
 D.
D.