题目内容
已知向量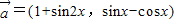 ,
,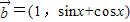 ,函数
,函数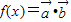 .
.(1)求f(x)的最大值及相应的x的值;
(2)若
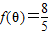 ,求
,求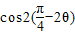 的值.
的值.
【答案】分析:(1)根据向量的数量积的运算法则可求得函数f(x)的解析式,进而利用二倍角公式和两角和公式化简整理利用正弦函数的性质求得函数的最大值和相应的x的值.
(2)根据(1)中函数的解析式和 求得
求得 两边平方利用同角三角函数的基本关系和二倍角公式求得sin4θ的值,最后利用诱导公式,把sin4θ的值代入即可.
两边平方利用同角三角函数的基本关系和二倍角公式求得sin4θ的值,最后利用诱导公式,把sin4θ的值代入即可.
解答:解:(1)因为 ,
, ,
,
所以f(x)=1+sin2x+sin2x-cos2x=1+sin2x-cos2x=
因此,当 ,即
,即 (k∈Z)时,f(x)取得最大值
(k∈Z)时,f(x)取得最大值 ;
;
(2)由f(θ)=1+sin2θ-cos2θ及 得
得 ,
,
两边平方得 ,即
,即 .
.
因此, .
.
点评:本题主要考查了利用两角和公式和二倍角公式化简求值,诱导公式的运用,平面向量的运算.考查了学生综合运用基础知识的能力.
(2)根据(1)中函数的解析式和
 求得
求得 两边平方利用同角三角函数的基本关系和二倍角公式求得sin4θ的值,最后利用诱导公式,把sin4θ的值代入即可.
两边平方利用同角三角函数的基本关系和二倍角公式求得sin4θ的值,最后利用诱导公式,把sin4θ的值代入即可.解答:解:(1)因为
 ,
, ,
,所以f(x)=1+sin2x+sin2x-cos2x=1+sin2x-cos2x=

因此,当
 ,即
,即 (k∈Z)时,f(x)取得最大值
(k∈Z)时,f(x)取得最大值 ;
;(2)由f(θ)=1+sin2θ-cos2θ及
 得
得 ,
,两边平方得
 ,即
,即 .
.因此,
 .
.点评:本题主要考查了利用两角和公式和二倍角公式化简求值,诱导公式的运用,平面向量的运算.考查了学生综合运用基础知识的能力.

练习册系列答案
相关题目
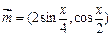 ,
, ,函数
,函数
 的最小正周期;
的最小正周期;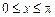 ,求
,求










 ,
, ,函数
,函数 .
. ,
, ,函数
,函数 .
. 在
在 上有解,求
上有解,求 的取值范围;
的取值范围; 中,
中, 分别是A,B,C所对的边,当(Ⅰ)中的
分别是A,B,C所对的边,当(Ⅰ)中的 时,求
时,求 的最小值.
的最小值. ,
, ,函数
,函数 .
. 的最小正周期以及单调递增区间;
的最小正周期以及单调递增区间; 时, 求
时, 求 在
在 内的所有实数根之和.
内的所有实数根之和.