Question

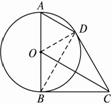
如图2-3-4所示，AB为⊙O的直径，BC、CD为⊙O的切线，B、D为切点，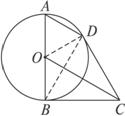

图2-3-4

（1）求证：AD∥OC；

（2）若⊙O的半径为1，求AD·OC的值.

Answer 1

思路分析：对于（1），连结OD、BD，证AD⊥BD，OC⊥BD；对于（2），连结BD，证△ABD∽△OCB即可.

（1）证明：连结OD、BD.

∵BC、CD是⊙O的切线，

∴OB⊥BC，OD⊥CD.

∴∠OBC=∠ODC=90°.

又∵OB=OD，OC=OC，

∴Rt△OBC≌Rt△ODC.

∴BC=CD.

∵OB=OD，∴OC⊥BD.

又∵AB为⊙O的直径，

∴∠ADB=90°,

即AD⊥BD.

∴AD∥OC.

（2）解：∵AD∥OC，∴∠A=∠BOC.

又∠ADB=∠OBC=90°，

∴△ABD∽△OCB.

∴.

∴AD·OC=AB·OB=2×1=2.