题目内容
9.求函数y=-2sin(3x-$\frac{π}{6}$)的周期,值域,求函数的对称中心,对称轴,单调递增区间.分析 代入周期公式即可求出周期,由系数为-2可知值域为[-2,2],令y=0即可解出对称中心的横坐标,令y=±2解出对称轴坐标,令$\frac{π}{2}$+2kπ≤3x-$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ可求出增区间.
解答 解:T=$\frac{2π}{3}$,
值域为[-2,2];
令y=0得sin(3x-$\frac{π}{6}$)=0,
∴3x-$\frac{π}{6}$=kπ,k∈Z.
解得x=$\frac{kπ}{3}+\frac{π}{18}$,k∈Z.
∴函数的对称中心为($\frac{kπ}{3}+\frac{π}{18}$,0).k∈Z.
令|sin(3x-$\frac{π}{6}$)|=1得3x-$\frac{π}{6}$=$\frac{π}{2}$+kπ,k∈Z.
解得x=$\frac{kπ}{3}$+$\frac{2π}{9}$,k∈Z.
∴函数的对称轴方程为x=$\frac{kπ}{3}$+$\frac{2π}{9}$,k∈Z.
令$\frac{π}{2}$+2kπ≤3x-$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,k∈Z.
解得$\frac{2kπ}{3}$+$\frac{2π}{9}$≤x≤$\frac{2kπ}{3}$+$\frac{5π}{9}$,k∈Z.
∴函数的单调递增区间为[$\frac{2kπ}{3}$+$\frac{2π}{9}$,$\frac{2kπ}{3}$+$\frac{5π}{9}$],k∈Z.
点评 本题考查了三角函数的周期,对称中心,对称轴,和单调区间,属于基础题.

练习册系列答案
相关题目
20.已知函数$f(x)=\left\{{\begin{array}{l}{(a-2)x+1,x<1}\\{{{(\frac{1}{2})}^x}-1,x≥1}\end{array}}\right.$是R上的单调递减函数,则实数a的取值范围是( )
| A. | (-∞,2) | B. | $(-∞,\frac{1}{2}]$ | C. | $[\frac{1}{2},2)$ | D. | (0,2) |
4.函数f(x)=x-ln|x|的图象为( )
| A. | 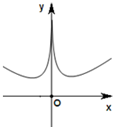 | B. |  | C. |  | D. |  |
 某校高二年级有1200人,从中抽取100名学生,对其期中考试语文成绩进行统计分析,得到如图所示的频率分布直方图,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校高二年级有1200人,从中抽取100名学生,对其期中考试语文成绩进行统计分析,得到如图所示的频率分布直方图,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].