题目内容
(本题满分12分)
已知函数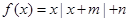 ,其中
,其中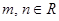
(1)
若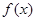 为R上的奇函数,求
为R上的奇函数,求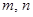 的值;
的值;
(2)
若常数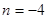 ,且
,且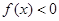 对任意
对任意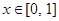 恒成立,求
恒成立,求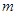 的取值范围.
的取值范围.
【答案】
(Ⅰ)
 (Ⅱ)
(Ⅱ) .
.
【解析】本试题主要是考查了函数的奇偶性以及函数与不等式的关系的运用。
(1)若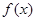 为奇函数,
为奇函数,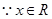 ,
, ,即
,即

 由
由 ,有
,有 ,
,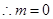 -
-
(2)常数 ,且
,且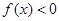 对任意
对任意 恒成立,则只需要研究函数的最大值小于零即可,得到参数m的范围。
恒成立,则只需要研究函数的最大值小于零即可,得到参数m的范围。
解:(Ⅰ)
若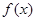 为奇函数,
为奇函数,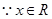 ,
, ,即
,即
 ,---2分
,---2分
 由
由 ,有
,有 ,
,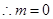 ---4分
---4分
此时,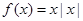 是R上的奇函数,故所求
是R上的奇函数,故所求 的值为
的值为
(Ⅱ) ① 当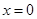 时,
时,  恒成立,
恒成立, ----6分
----6分
② 当 时,原不等式可变形为
时,原不等式可变形为 即
即 恒成立—7分
恒成立—7分
∴ 只需对 ,满足
,满足
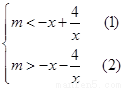 恒成立-----9分
恒成立-----9分
对(1)式:令 ,当
,当 时,
时, ,
,
则 在
在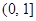 上单调递减,
上单调递减,
对(2)式:令 ,当
,当 时,
时, ,
,
则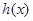 在
在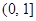 上单调递增,
上单调递增, ---11分
---11分
由①、②可知,所求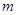 的取值范围是
的取值范围是
 .---12分
.---12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面