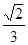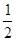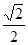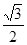题目内容
过点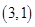 作圆
作圆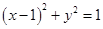 的两条切线,切点分别为
的两条切线,切点分别为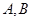 ,则直线
,则直线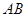 的方程为( )
的方程为( )
A.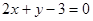 | B.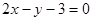 |
C.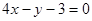 | D.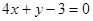 |
A
解析

练习册系列答案
相关题目
已知 ,
,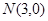 ,直线
,直线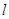 过点
过点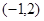 且与线段
且与线段 相交,则直线
相交,则直线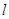 的斜率
的斜率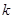 的取值范围是( )
的取值范围是( )
A.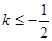 或 或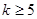 | B.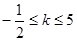 | C.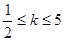 | D.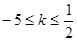 |
已知a,b满足a+2b=1,则直线ax+3y+b=0必过定点( )
A.(-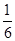 , ,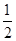 ) ) | B. (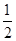 , ,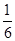 ) ) | C. (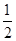 , - , -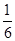 ) ) | D. (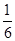 , - , -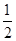 ) ) |
已知直线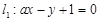 与
与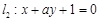 ,给出如下结论:
,给出如下结论:
①不论 为何值时,
为何值时,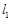 与
与 都互相垂直;
都互相垂直;
②当 变化时,
变化时, 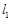 与
与 分别经过定点A(0,1)和B(-1,0);
分别经过定点A(0,1)和B(-1,0);
③不论 为何值时,
为何值时, 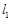 与
与 都关于直线
都关于直线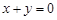 对称;
对称;
④当 变化时,
变化时, 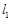 与
与 的交点轨迹是以AB为直径的圆(除去原点).
的交点轨迹是以AB为直径的圆(除去原点).
其中正确的结论有( ).
| A.①③ | B.①②④ | C.①③④ | D.①②③④ |
点 为圆
为圆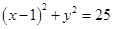 的弦
的弦 的中点,则直线
的中点,则直线 的方程为
的方程为
A. | B. |
C. | D.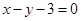 |
与直线l : y=2x+3平行,且与圆x2+y2-2x-4y+4=0相切的直线方程是( ).
A.x-y±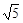 =0 =0 | B.2x-y+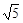 =0 =0 |
C.2x-y-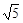 =0 =0 | D.2x-y±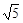 =0 =0 |
直线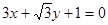 的倾斜角是( )
的倾斜角是( )
| A.300 | B.600 | C.1200 | D.1350 |
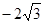 B.0 C.
B.0 C.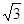 D.
D. 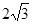
 是椭圆长轴的两个端点,
是椭圆长轴的两个端点,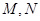 是椭圆上关于
是椭圆上关于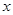 轴对称的两点,直线
轴对称的两点,直线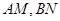 的斜率分别为
的斜率分别为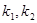 ,且
,且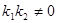 。若
。若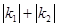 的最小值为1,则椭圆的离心率为
的最小值为1,则椭圆的离心率为