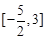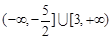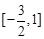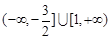题目内容
已知 是椭圆长轴的两个端点,
是椭圆长轴的两个端点,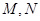 是椭圆上关于
是椭圆上关于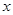 轴对称的两点,直线
轴对称的两点,直线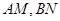 的斜率分别为
的斜率分别为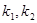 ,且
,且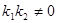 。若
。若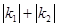 的最小值为1,则椭圆的离心率为
的最小值为1,则椭圆的离心率为
A.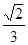 | B.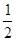 | C.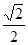 | D.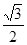 |
D
解析试题分析:先假设出点M,N,A,B的坐标,然后表示出两斜率的关系,再由|k1|+|k2|的最小值为1运用基本不等式的知识可得到当x0=0时可取到最小值,进而找到a,b,c的关系,进而可求得离心率的值.
当且仅当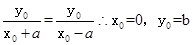 取得等号,
取得等号,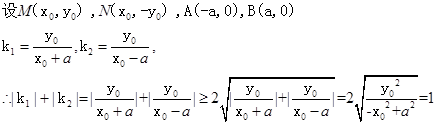
故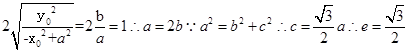 ,故选D.
,故选D.
考点:直线与椭圆的位置关系的运用
点评:本题主要考查椭圆的基本性质和基本不等式的应用.圆锥曲线是高考的重点问题,基本不等式在解决最值时有重要作用,所以这两方面的知识都很重要,一定要强化复习.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则 ( )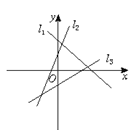
| A.k1<k2<k3 | B.k3<k1<k2 | C.k3<k2<k1 | D.k1<k3<k2 |
已知菱形 的两个顶点坐标:
的两个顶点坐标: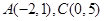 ,则对角线
,则对角线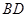 所在直线方程为
所在直线方程为
A.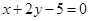 | B.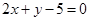 | C.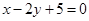 | D. |
已知直线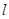 的方程为
的方程为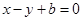
 ,则直线
,则直线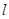 的倾斜角为( )
的倾斜角为( )
A.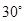 | B.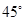 | C.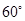 | D.与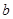 有关 有关 |
已知直线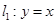 ,若直线
,若直线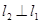 ,则直线
,则直线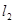 的倾斜角为
的倾斜角为
A.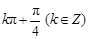 | B.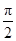 | C.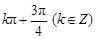 | D.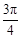 |
两直线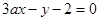 和
和 分别过定点A,B,则
分别过定点A,B,则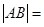 ( )
( )
A.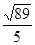 | B.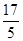 | C. | D.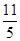 |
若直线经过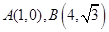 两点,则直线
两点,则直线 的倾斜角为
的倾斜角为
A.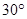 | B.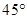 | C. | D.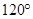 |
过点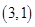 作圆
作圆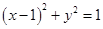 的两条切线,切点分别为
的两条切线,切点分别为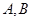 ,则直线
,则直线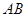 的方程为( )
的方程为( )
A.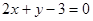 | B.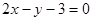 |
C.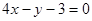 | D.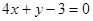 |
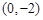 的直线L与以
的直线L与以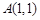 、
、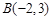 为端点的线段有公共点,则直线L的斜率k的取值范围是( )
为端点的线段有公共点,则直线L的斜率k的取值范围是( )