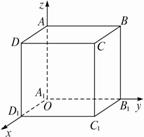
题目内容
如图，空间直角坐标系O-xyz中，已知A（1，0，0），B（0，2，0），现将△AOB按向量| p |
| 3 |
（Ⅰ）写出三点A'、O'、B'的坐标；
（Ⅱ）求证：AB'⊥BO'；
（Ⅲ）求二面角A-BB'-O的大小．
分析：（Ⅰ）先分别写出
，
，
的坐标，即可得到点A'、O'、B'的坐标；
（Ⅱ） 要证AB'⊥BO'；只需证明对应的数量积为0即可；
（Ⅲ） 先求平面的法向量，再利用向量的数量积公式求面面角．
| OA′ |
| OB′ |
| OO/ |
（Ⅱ） 要证AB'⊥BO'；只需证明对应的数量积为0即可；
（Ⅲ） 先求平面的法向量，再利用向量的数量积公式求面面角．
解答：解：（Ⅰ）
=
+
=
+
=（1，0，0）+（0，-1，
)=(1，-1，
)，
同理
=(0，2，0）+（0，-1，
)=（0，1，
)，又
=
=(0，-1，
)，
所以A'（1，-1，
)，O'（0，-1，
)，B'（0，1，
)；
（Ⅱ）证明：由（Ⅰ）
=(0，1，
)-(1，0，0）=（-1，1，
)，
=(0，-1，
)-(0，2，0）=（0，-3，
)，
而
•
=(-1)×0+1×(-3)+
×
=0，所以
⊥
，即AB'⊥BO'；
（Ⅲ）设平面ABB'的法向量为
=(x，y，z），则
⊥
且
⊥
，
所以
•
=0且
•
=0，即
，取z=1，得x=2
，y=
，
所以
=(2
，
，1）．又平面OBB'的一个法向量是
=(1，0，0），cos＜
，
＞=
=
=
，
所以＜
，
＞=30°，从而二面角A-BB'-O的大小为30°．
| OA′ |
| OA |
| AA′ |
| OA |
| p |
| 3 |
| 3 |
同理
| OB′ |
| 3 |
| 3 |
| OO′ |
| p |
| 3 |
所以A'（1，-1，
| 3 |
| 3 |
| 3 |
（Ⅱ）证明：由（Ⅰ）
| AB′ |
| 3 |
| 3 |
| BO′ |
| 3 |
| 3 |
而
| AB′ |
| BO′ |
| 3 |
| 3 |
| AB′ |
| BO′ |
（Ⅲ）设平面ABB'的法向量为
| m |
| m |
| BB′ |
| m |
| AB′ |
所以
| m |
| BB′ |
| m |
| AB′ |
|
| 3 |
| 3 |
所以
| m |
| 3 |
| 3 |
| n |
| m |
| n |
| ||||
|
|
2
| ||||||
|
| ||
| 2 |
所以＜
| m |
| n |
点评：本题的考点是用空间向量求平面角的夹角，主要考查空间向量的运用，考查向量的数量积公式，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
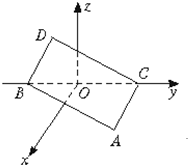如图在空间直角坐标系中BC=2，原点O是BC的中点，点A的坐标是（
，原点
是
的中点，点
的坐标是（
），点
在平面
上，且
，
．
的坐标；
和
的夹角为
，求
的值．
