题目内容
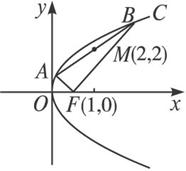
已知
2 设A(x1,y1),B(x2,y2),
∴y12=4x1,
y22=4x2.
两式相减得(y1+y2)(y1-y2)=4(x1-x2).
又y1+y2=2×2=4,
∴![]() ,
,
即kAB=1.
∴lAB:y-2=x-2,即y=x.
∴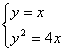
![]() x2-4x=0.
x2-4x=0.
∴x1+x2=4,x1x2=0.
∴|AB|=![]() =
=![]() =
=![]() .
.
点F到AB的距离d=![]() .
.
∴S△ABF=![]() ×
×![]() ×
×![]() =2.
=2.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
已知
2 设A(x1,y1),B(x2,y2),

∴y12=4x1,
y22=4x2.
两式相减得(y1+y2)(y1-y2)=4(x1-x2).
又y1+y2=2×2=4,
∴![]() ,
,
即kAB=1.
∴lAB:y-2=x-2,即y=x.
∴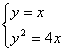
![]() x2-4x=0.
x2-4x=0.
∴x1+x2=4,x1x2=0.
∴|AB|=![]() =
=![]() =
=![]() .
.
点F到AB的距离d=![]() .
.
∴S△ABF=![]() ×
×![]() ×
×![]() =2.
=2.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案