题目内容
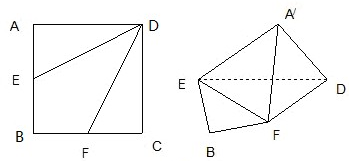
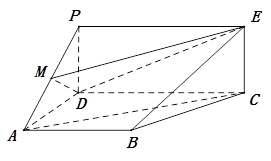
将棱长为 的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点
的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点 分别是
分别是 的中点.
的中点.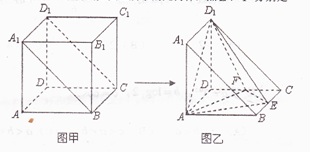
(Ⅰ)证明: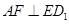 ;
;
(Ⅱ)求三棱锥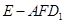 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)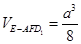 .
.
解析试题分析:(Ⅰ)证明: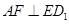 ,证明两线垂直,只需证一线垂直另一线所在的平面,因此本题的关键是找平面,注意到过
,证明两线垂直,只需证一线垂直另一线所在的平面,因此本题的关键是找平面,注意到过 的线中
的线中 ,可考虑连接
,可考虑连接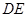 ,看
,看 是否垂直平面
是否垂直平面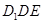 ,因此本题转化为只要证明
,因此本题转化为只要证明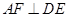 即可,由平面几何知识易证;(Ⅱ)求棱锥
即可,由平面几何知识易证;(Ⅱ)求棱锥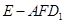 的体积,直接求,底面面积及高都不好求,但注意到棱锥
的体积,直接求,底面面积及高都不好求,但注意到棱锥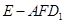 与棱锥
与棱锥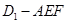 是一个几何体,而这个棱锥的高为
是一个几何体,而这个棱锥的高为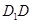 ,而
,而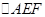 的面积
的面积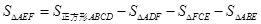 ,故体积容易求,值得注意的是,当一个几何体的体积不好求是,可进行转化成其它几何体来求.
,故体积容易求,值得注意的是,当一个几何体的体积不好求是,可进行转化成其它几何体来求.
试题解析:(Ⅰ)证:连接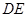 ,交
,交 于点
于点 ,∵
,∵ 平面
平面 ,
, 平面
平面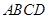 ,∴
,∴ ,
, 
∵点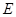 ,
, 分别是
分别是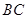 ,
, 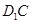 的中点, ∴
的中点, ∴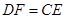 , 又∵
, 又∵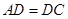 ,
,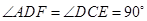 ,∴
,∴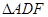 ≌
≌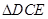 ,∴
,∴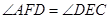 ,又∵
,又∵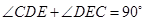 ,∴
,∴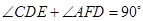 ,
,
∴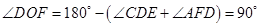 ,即
,即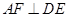 ,又∵
,又∵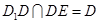 ,∴
,∴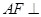 平面
平面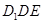 ,
,
又∵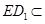 平面
平面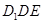 ,∴
,∴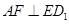 ;
;
(Ⅱ)解:∵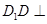 平面
平面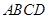 ,∴
,∴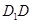 是三棱锥
是三棱锥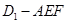 的高,且
的高,且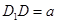 ,
,
∵点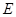 ,
, 分别是
分别是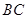 ,
,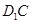 的中点,∴
的中点,∴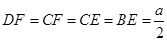 ,∴
,∴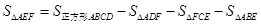
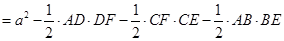
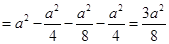 ,∴
,∴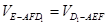

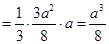
考点:线线垂直的判定、线面垂直的判定、以及棱锥的体积公式.

练习册系列答案
相关题目
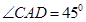 .
.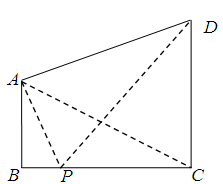
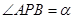 ,
, ,问点P在何处时,
,问点P在何处时,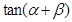 最小?
最小?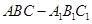 中,
中,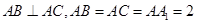 ,点
,点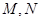 分别为
分别为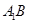 和
和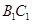 的中点.
的中点.
 平面
平面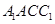 ;
;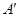
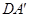 ⊥EF;
⊥EF;
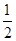 CD=1,PD=
CD=1,PD= 。
。
 ?
? 中,
中, ,点D是AB的中点,
,点D是AB的中点,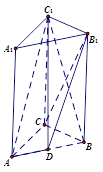
 ; (2)
; (2)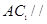 平面
平面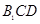
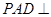 平面
平面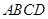 ,
,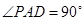 ,且
,且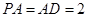 ,
, 、
、 、
、 分别是线段
分别是线段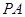 、
、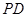 、
、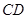 的中点.
的中点.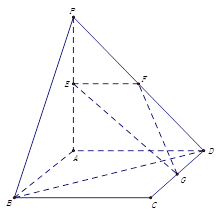
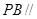 平面
平面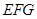 ;
;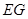 、
、 所成角的余弦值.
所成角的余弦值. 中,四边形
中,四边形 是菱形,
是菱形, ,E为PB的中点.
,E为PB的中点.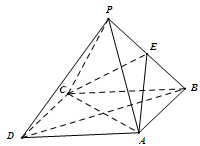
 平面
平面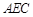 ;
;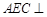 平面
平面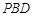 .
.