题目内容
点 是曲线
是曲线 上的任意一点,则点
上的任意一点,则点 到直线
到直线 的最小距离为
的最小距离为
 是曲线
是曲线 上的任意一点,则点
上的任意一点,则点 到直线
到直线 的最小距离为
的最小距离为| A.1 | B. | C. | D.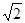 |
D
分析:由题意知,当曲线上过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小,求出曲线对应的函数的导数,令导数值等于1,可得且点的坐标,此切点到直线y=x-2的距离即为所求.
解:点P是曲线y=x2-lnx上任意一点,
当过点P的切线和直线y=x-2平行时,
点P到直线y=x-2的距离最小.
直线y=x-2的斜率等于1,
令y=x2-lnx的导数 y′=2x-
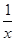 =1,x=1,或 x=-
=1,x=1,或 x=- (舍去),
(舍去),故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
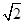 ,
,故点P到直线y=x-2的最小距离为
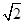 ,
,故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
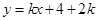 与曲线
与曲线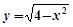 有两个交点,则k的取值范围是( )
有两个交点,则k的取值范围是( ) )
) 入射到直线
入射到直线 后反射,则反射光线所在的直线方程为( )
后反射,则反射光线所在的直线方程为( )



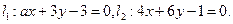 若
若 ,则
,则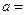 ________;
________;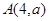 和
和 的直线与直线
的直线与直线 平行,则
平行,则 的值( )
的值( ) 
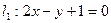 与
与 的位置关系为 ▲ .
的位置关系为 ▲ .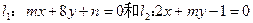 ,试确定
,试确定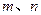 的值,使得:
的值,使得: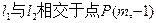 ; (2)
; (2)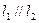
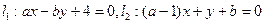 ,求满足下列条件的
,求满足下列条件的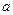 、
、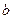 的值.直线
的值.直线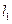 过点
过点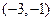 ,并且直线
,并且直线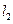 垂直;
垂直;