题目内容
平面直角坐标系xOy中,动点P从点P0(4,0)出发,运动过程中,到定点F(-2,0)的距离与到定直线l:x=-8的距离之比为常数.①求点P的轨迹方程;
②在轨迹上是否存在点M(s,t),使得以M为圆心且经过定点F(-2,0)的圆与直线x=8相交于两点A、B?若存在,求s的取值范围;若不存在,说明理由.
分析:①直接代入公式即可求得点P的轨迹方程;
②先把圆与直线x=8相交于两点转化为圆心M到直线x=8的距离小于圆的半径|MF|;再借助于①的结果即可求s的取值范围.
②先把圆与直线x=8相交于两点转化为圆心M到直线x=8的距离小于圆的半径|MF|;再借助于①的结果即可求s的取值范围.
解答:解:①设P(x,y)是轨迹上任意一点,根据两点距离公式和点到直线距离公式,依题意有,
=
=
,化简得
+
=1.
②“圆与直线x=8相交于两点”当且仅当圆心M到直线x=8的距离小于圆的半径|MF|,|s-8|<|MF|,
由①知|MF|=
|s+8|,
所以|s-8|<
|s+8|,
又由①知-4≤s≤4,
所以8-s<
(s+8),解得
<s≤4.
| ||
| |x+8| |
| 4+2 |
| 4+8 |
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
②“圆与直线x=8相交于两点”当且仅当圆心M到直线x=8的距离小于圆的半径|MF|,|s-8|<|MF|,
由①知|MF|=
| 1 |
| 2 |
所以|s-8|<
| 1 |
| 2 |
又由①知-4≤s≤4,
所以8-s<
| 1 |
| 2 |
| 8 |
| 3 |
点评:本题是椭圆与圆的综合,解题要求先用轨迹法求轨迹方程,再讨论动点的几何性质,关键是数形结合,将方程中数量的几何意义应用于曲线几何属性的量化,将①的结果自然地应用于②的求解.

练习册系列答案
相关题目
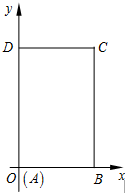 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.