题目内容
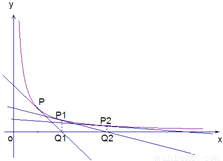
如图,已知曲线C: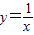 在点P(1,1)处的切线与x轴交于点Q1,过点Q1作x轴的垂线交曲线C于点P1,曲线C在点P1处的切线与x轴交于点Q2,过点Q2作x轴的垂线交曲线C于点P2,…,依次得到一系列点P1、P2、…、Pn,设点Pn的坐标为(xn,yn)(n∈N*).
在点P(1,1)处的切线与x轴交于点Q1,过点Q1作x轴的垂线交曲线C于点P1,曲线C在点P1处的切线与x轴交于点Q2,过点Q2作x轴的垂线交曲线C于点P2,…,依次得到一系列点P1、P2、…、Pn,设点Pn的坐标为(xn,yn)(n∈N*).(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)求三角形OPnPn+1的面积
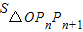
(Ⅲ)设直线OPn的斜率为kn,求数列{nkn}的前n项和Sn,并证明
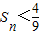 .
.
【答案】分析:(Ⅰ)通过求导即可得到切线的斜率,进而得到切线的方程,即可得到xn+1与xn的关系,利用等比数列的通项公式即可求出.
(Ⅱ)利用三角形的面积公式、梯形的面积公式及(Ⅰ)的结论即可得出;
(Ⅲ)利用(Ⅰ)的结论即可求出nkn,再利用“错位相减法”即可求出Sn,进而证明结论.
解答:解:(Ⅰ)∵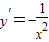 ,∴f′(1)=-1,
,∴f′(1)=-1,
∴曲线C: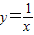 在点P(1,1)处的切线为y-1=-(x-1),
在点P(1,1)处的切线为y-1=-(x-1),
令y=0,则x=2,∴Q1(2,0),∴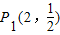 ,∴x1=2.
,∴x1=2.
则过点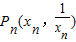 的切线斜率为
的切线斜率为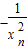 ,其方程为
,其方程为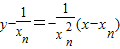 ,
,
令y=0,得到x=2xn,∴Qn+1(2xn,0),即xn+1=2xn,∴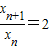 .
.
∴数列{xn}是以2为首项,2为公比的等比数列,
∴ .
.
(Ⅱ)∵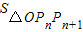 =
=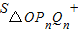
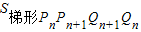 -
-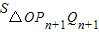
=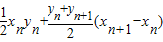 -
-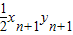
=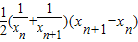 =
=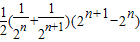 =
= .
.
(Ⅲ)证明:由(1)可知:kn=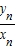 =
=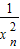 =
=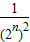 =
=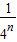 ,∴nkn=
,∴nkn=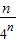 .
.
∴Sn=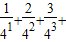 …+
…+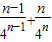 ,
,
4Sn=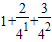 +…+
+…+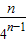 ,
,
两式相减得3Sn═1+ +
+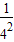 +…+
+…+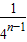 -
-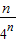 =
=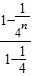 -
-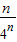 ,
,
∴Sn=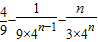
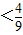 .
.
故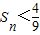 成立.
成立.
点评:熟练掌握导数的几何意义、等比数列的通项公式及其前n项和公式、“错位相减法”是解题的关键.
(Ⅱ)利用三角形的面积公式、梯形的面积公式及(Ⅰ)的结论即可得出;
(Ⅲ)利用(Ⅰ)的结论即可求出nkn,再利用“错位相减法”即可求出Sn,进而证明结论.
解答:解:(Ⅰ)∵
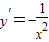 ,∴f′(1)=-1,
,∴f′(1)=-1,∴曲线C:
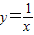 在点P(1,1)处的切线为y-1=-(x-1),
在点P(1,1)处的切线为y-1=-(x-1),令y=0,则x=2,∴Q1(2,0),∴
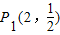 ,∴x1=2.
,∴x1=2.则过点
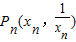 的切线斜率为
的切线斜率为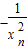 ,其方程为
,其方程为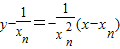 ,
,令y=0,得到x=2xn,∴Qn+1(2xn,0),即xn+1=2xn,∴
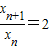 .
.∴数列{xn}是以2为首项,2为公比的等比数列,
∴
 .
.(Ⅱ)∵
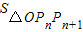 =
=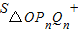
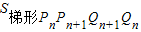 -
-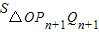
=
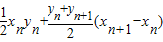 -
-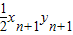
=
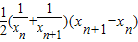 =
=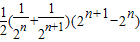 =
= .
.(Ⅲ)证明:由(1)可知:kn=
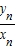 =
=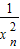 =
=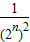 =
=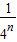 ,∴nkn=
,∴nkn=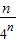 .
.∴Sn=
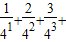 …+
…+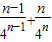 ,
,4Sn=
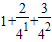 +…+
+…+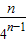 ,
,两式相减得3Sn═1+
 +
+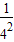 +…+
+…+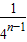 -
-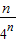 =
=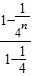 -
-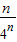 ,
,∴Sn=
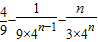
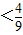 .
.故
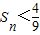 成立.
成立.点评:熟练掌握导数的几何意义、等比数列的通项公式及其前n项和公式、“错位相减法”是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,已知曲线C:
如图,已知曲线C: 如图,已知椭圆C:
如图,已知椭圆C: 如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).
如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).