题目内容
用边长为48厘米的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒.当所做的铁盒的容积最大时,在四角截去的正方形的边长为( )
| A.12 | B.10 | C.8 | D.6 |
C
解析试题分析:设在四角截去的正方形的边长为 ,则铁盒容积为
,则铁盒容积为 ,而
,而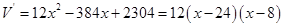 ,即
,即 的单调递增区间为
的单调递增区间为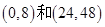 ,单调递减区间为
,单调递减区间为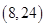 ,所以在
,所以在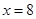 时V有极大值.
时V有极大值.
考点:导函数的应用、函数思想.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
若曲线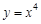 的一条切线l与直线
的一条切线l与直线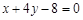 垂直,则切线l的方程为 ( )
垂直,则切线l的方程为 ( )
A.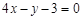 | B.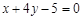 |
C.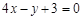 | D.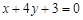 |
如图,函数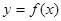 在
在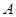 ,
, 两点间的平均变化率是( )
两点间的平均变化率是( )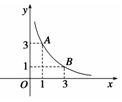
| A.1 | B.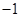 | C.2 | D.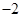 |
可导函数 的导函数为
的导函数为 ,且满足:①
,且满足:① ;②
;② ,记
,记 ,
,  ,
, 则
则 的大小顺序为( )
的大小顺序为( )
A. | B. | C. | D. |
已知函数f(x)在R上满足 ,则曲线y=f(x)在点 (1,f(1))处切线的斜率是 ( )
,则曲线y=f(x)在点 (1,f(1))处切线的斜率是 ( )
| A.2 | B.1 | C.3 | D.-2 |
过曲线y=x3+x-2上一点P0处的切线平行于直线y=4x,则点P0的一个坐标是( )
| A.(0,-2) | B.(1,1) | C.(1,4) | D.(-1,-4) |
已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( ).
| A.当k=1时,f(x)在x=1处取到极小值 |
| B.当k=1时,f(x)在x=1处取到极大值 |
| C.当k=2时,f(x)在x=1处取到极小值 |
| D.当k=2时,f(x)在x=1处取到极大值 |
若点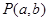 在函数
在函数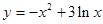 的图像上,点
的图像上,点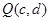 在函数
在函数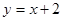 的图像上,则
的图像上,则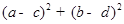 的最小值为( )
的最小值为( )
A.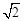 | B.2 | C.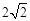 | D.8 |
 在区间
在区间 上存在
上存在 ,满足
,满足 则称函数
则称函数 是区间
是区间 上的双中值函数,则实数
上的双中值函数,则实数 的取值范围是 ( )
的取值范围是 ( )


