题目内容
若曲线y=Asinωx+a(A>0,ω>0)在区间 上截直线y=2与y=-1所得的弦长相等且不为0,则下列对a和A的描述正确的是( )
上截直线y=2与y=-1所得的弦长相等且不为0,则下列对a和A的描述正确的是( )A.

B.a=1,A>1
C.
 ≤
≤
D.a=1,A≤1
【答案】分析:曲线y=Asinωx+a(A>0,ω>0)的性质知,在一个周期上截直线y=2与y=-1所得的弦长相等且不为0,可知两条直线关于y=a对称,由此对称性可求出a,又截得的弦长不为0,故可得振幅大于 .
.
解答:解:由题意曲线y=Asinωx+a(A>0,ω>0)的图象关于直线y=a的对称
又截直线y=2及y=-1所得的弦长相等
所以,两条直线y=2及y=-1关于y=a对称
a=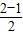 =
=
又弦长相等且不为0
故振幅A大于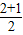 =
=
A>
故有a= ,A>
,A>
故应选A.
点评:本题考点y=Asin(ωx+φ)中参数的物理意义,考查三角函数的图象的性质及其与相应参数的关系,考查对三角函数图象的特征理解的能力.
 .
.解答:解:由题意曲线y=Asinωx+a(A>0,ω>0)的图象关于直线y=a的对称
又截直线y=2及y=-1所得的弦长相等
所以,两条直线y=2及y=-1关于y=a对称
a=
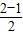 =
=
又弦长相等且不为0
故振幅A大于
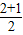 =
=
A>

故有a=
 ,A>
,A>
故应选A.
点评:本题考点y=Asin(ωx+φ)中参数的物理意义,考查三角函数的图象的性质及其与相应参数的关系,考查对三角函数图象的特征理解的能力.

练习册系列答案
相关题目
若曲线y=Asinωx+a(A>0,ω>0)在区间[0,
]上截直线y=2与y=-1所得的弦长相等且不为0,则下列对a和A的描述正确的是( )
| 2π |
| ω |
A、a=
| ||||
| B、a=1,A>1 | ||||
C、a=
| ||||
| D、a=1,A≤1 |
 上截直线y=2与y=-1所得的弦长相等且不为0,则下列对a和A的描述正确的是( )
上截直线y=2与y=-1所得的弦长相等且不为0,则下列对a和A的描述正确的是( )
 ≤
≤
 上截直线y=2与y=-1所得的弦长相等且不为0,则下列对a和A的描述正确的是( )
上截直线y=2与y=-1所得的弦长相等且不为0,则下列对a和A的描述正确的是( )
 ≤
≤