题目内容
已知点P在曲线![]() 上,曲线C在点P的切线与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
上,曲线C在点P的切线与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
(1)求f(t)的解析式;
(2)设数列{an}(n≥1,n∈N)满足a1=1,an=f(![]() )(n≥2),求数列{an}的通项公式;
)(n≥2),求数列{an}的通项公式;
(3)在(2)的条件下,当1<k<3时,证明不等式:a1+a2+a3…an>![]() .
.
答案:
解析:
解析:
|
(1) ∴曲线C在P点的切线斜率为 则该切线方程为 由 因此, (2) 即 ①当 ②当 又 (3) 故不等式 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
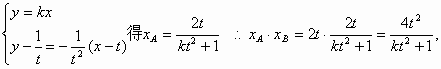
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, ,|AN|=3,且|BN|=6.
,|AN|=3,且|BN|=6.