题目内容
已知F1、F2为双曲线C:x²-y²=2的左、右焦点,点P在C上,|PF1|=|2PF2|,则cos∠F1PF2=
(A)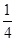 (B)
(B)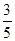 (C)
(C)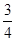 (D)
(D)
【解析】双曲线的方程为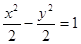 ,所以
,所以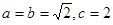 ,因为|PF1|=|2PF2|,所以点P在双曲线的右支上,则有|PF1|-|PF2|=2a=
,因为|PF1|=|2PF2|,所以点P在双曲线的右支上,则有|PF1|-|PF2|=2a=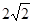 ,所以解得|PF2|=
,所以解得|PF2|=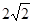 ,|PF1|=
,|PF1|=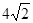 ,所以根据余弦定理得
,所以根据余弦定理得 ,选C.
,选C.
【答案】
C

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )