题目内容
(14分)求函数y＝x3＋x2－x在区间[－2,1]上的最大值与最小值．
【答案】
解：y′＝3x2＋2x－1，令y′＝3x2＋2x－1＝0得，x1＝－1，x2＝
函数的最大值为1，最小值为－2．
【解析】由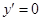
得函数的极值点，然后求出端点值，再与极值比较确定最大值和最小值.
解：y′＝3x2＋2x－1，令y′＝3x2＋2x－1＝0得，x1＝－1，x2＝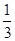
．
f(－1)＝1，f()＝－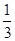
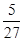，f(－2)＝－2，f(1)＝1．
所以函数的最大值为1，最小值为－2．
练习册系列答案
相关题目
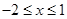上的最小值为
，
(A＞0，
＞0，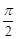
＜
＜
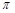)，x∈[－3，0]的图象，且图象的最高点为B(－1，
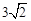)；赛道的中间部分为
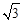千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧
．
，求当“矩形草坪”的面积最大时
(A＞0，
＞0，
＜
＜
)，x∈[－3，0]的图象，且图象的最高点为B(－1，
)；赛道的中间部分为
千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧
．
，求当“矩形草坪”的面积最大时
，Tn为数列{bn}的前n项和，试比较4Sn与Tn的大小。