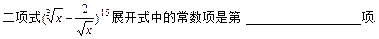题目内容

在（1+x）3+（1+x）4+…+（1+x）n+2的展开式中，含x2项的系数是多少？
（1+x）3中含x2项的系数是C32（1+x）4中含x2项的系数是C42…
（1+x）n+2中含x2项的系数是Cn+22
所以，所求展开式中含x2项的系数是：
C32+C42+…+Cn+22=（C33+C32+C42+…+Cn+22）-C33=Cn+33-C33=
n(n2+6n+11)
6
练习册系列答案
相关题目
已知在(
3x
-
1
2
3x
)n的展开式中，第5项为常数项．
（1）求n；
（2）求展开式中含x2的项．
在(x2-
1
2x
)n的展开式中，求：所有的二项式系数之和与各项系数之和的比为218，求该二项式展开式中的
（1）第6项；（2）第3项的系数；（3）常数项．
已知(1-2x)n=a0+a1x+a2x2+…+anxn，且a3：a5=1：4．
（Ⅰ）求a0+a1+a2+…+an；
（Ⅱ）求(x+
1
3x
)n中的常数项．
若（x2+
1
ax
）6的二项展开式中x3的系数为
5
2
，则a=（　　）
A．1B．2C．3D．4
在二项式（x-
1
x2
）6的展开式中，常数项是（　　）
A．-10B．-15C．10D．15
已知（
x
+
1
2•
4x
）n的展开式前三项中的x的系数成等差数列．
（1）展开式中所有的x的有理项为第几项？
（2）求展开式中系数最大的项．
某电视台的一个智力游戏节目中，有一道将中国四大名著《三国演义》、《水浒传》、《西游记》、《红楼梦》与它们的作者连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线，每连对一个得2分，连错得－1分，某观众只知道《三国演义》的作者是罗贯中，其他不知道随意连线，将他的得分记作ξ.
(1)求该观众得分ξ为负数的概率；
(2)求ξ的分布列．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网