题目内容
18.已知z=cosθ+(1-sinθ)i,α∈[0,2π],i为虚数单位,则|z|的取值范围是[0,2].分析 直接利用复数模的计算公式写出复数的模,然后结合三角运算求得答案.
解答 解:∵z=cosθ+(1-sinθ)i,
∴|z|=$\sqrt{co{s}^{2}θ+(1-sinθ)^{2}}$=$\sqrt{co{s}^{2}θ+1-2sinθ+si{n}^{2}θ}$=$\sqrt{2-2sinθ}$.
∵θ∈[0,2π],∴-2≤2sinθ≤2,则0≤2-2sinθ≤4,
∴|z|的取值范围是[0,2].
故答案为:[0,2].
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列说法中,不正确的是( )
| A. | 已知a,b,m∈R,命题“若am2<bm2,则a<b”为真命题 | |
| B. | 命题“?x0∈R,x02-x0>0”的否定是:“?x∈R,x2-x≤0” | |
| C. | 命题“p或q”为真命题,则命题p和q命题均为真命题 | |
| D. | “x>3”是“x>2”的充分不必要条件 |
10.在复平面内,复数z=1-2i对应的点的坐标为( )
| A. | (1,2) | B. | (2,1) | C. | (1,-2) | D. | (2,-1) |
7.已知i是虚数单位,复数$\frac{1+i}{2-i}$=( )
| A. | $\frac{1}{5}-\frac{3}{5}$i | B. | $\frac{3}{5}+\frac{1}{5}$i | C. | $\frac{1}{3}+\frac{2}{3}$i | D. | $\frac{1}{5}+\frac{3}{5}$i |
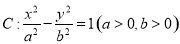 的右焦点为
的右焦点为 ,直线
,直线 与双曲线
与双曲线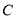 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为 为坐标原点,若
为坐标原点,若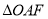 的面积为
的面积为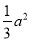 ,则双曲线
,则双曲线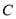 的离心率为( )
的离心率为( ) B.
B.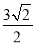
 D.
D.


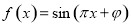 的部分图象如图所示,点
的部分图象如图所示,点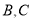 是该图象与
是该图象与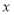 轴的交点,过点
轴的交点,过点 的直线与该图象交于
的直线与该图象交于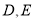 两点,则
两点,则 的值为( )
的值为( )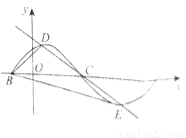

 D.2
D.2