题目内容
【题目】已知实数a>0, ![]() 方程
方程 ![]() 有且仅有两个不等实根,且较大的实根大于3,则实数a的取值范围 .
有且仅有两个不等实根,且较大的实根大于3,则实数a的取值范围 .
【答案】![]()
【解析】解:设比较大的根为x1 , 则x1>3, 此时由 ![]() =log3x>log33=1,
=log3x>log33=1,
即a ![]() ,即a
,即a ![]() .
.
∵方程 ![]() 有且仅有两个不等实根,
有且仅有两个不等实根,
∴当x≤1时,方程 ![]() 有且仅有1实根,
有且仅有1实根,
即﹣x ![]() ,在x≤1时,只有一个根.
,在x≤1时,只有一个根.
∴x ![]() ,
,
设g(x)=x ![]() ,(x≤1),
,(x≤1),
函数的对称轴为x=a,
若a≥1,
∵g(0)= ![]() ,
,
∴此时满足g(1)≤0,(图1)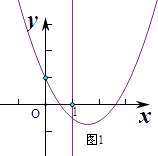
即g(1)=1﹣2a+ ![]() ≤0,
≤0,
∴7a2﹣32a+16≤0,
解得 ![]() ,∴此时1≤a≤4,.
,∴此时1≤a≤4,.
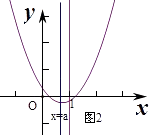
若0<a<1,
∵g(0)= ![]() ,
,
∴此时满足g(1)<0,
即g(1)=1﹣2a+ ![]() <0,
<0,
∴77a2﹣32a+16<0,
解得 ![]() ,∴此时
,∴此时 ![]() ,
,
∴ ![]() ,
,
又a ![]() ,
,
∴ ![]() ,
,
即实数a的取值范围是 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】关于本题考查的函数的零点与方程根的关系和函数的零点,需要了解二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能得出正确答案.

练习册系列答案
相关题目