题目内容
(选修4-1 几何证明选讲)
如图,已知:C是以AB为直径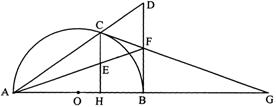 的半圆O上一点,
的半圆O上一点,
CH⊥AB于点H,直线AC与过B点的切线相交于
点D,E为CH中点,连接AE并延长交BD于点F,
直线CF交直线AB于点G.
(Ⅰ)求证:F是BD的中点;
(Ⅱ)求证:CG是⊙O的切线.
(1)略(2)略
解析:
(Ⅰ)证:∵CH⊥AB,DB⊥AB,∴△AEH∽AFB,△ACE∽△ADF
∴![]() ,∵HE=EC,∴BF=FD ∴ F是BD中点.……………………(5分)
,∵HE=EC,∴BF=FD ∴ F是BD中点.……………………(5分)
(Ⅱ)∵AB是直径,∴∠ACB=90°∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO
∴∠OCF=90°,∴CG是⊙O的切线……………………………………………(10分)
(说明:也可证明△OCF≌△OBF(从略,仿上述评分标准给分))
点评:本题考查相似三角形判断及其性质,圆的切线的判断,属于容易题。

练习册系列答案
相关题目
 (选修4-1 几何证明选讲)(本题满分10分)
(选修4-1 几何证明选讲)(本题满分10分)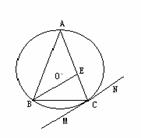
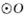 的弦,C、F是
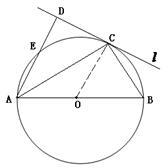
的弦,C、F是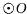 上的点,OC垂直于弦AB,过点F作
上的点,OC垂直于弦AB,过点F作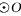 的切线,交AB的延长线于D,连结CF交AB于点E.
的切线,交AB的延长线于D,连结CF交AB于点E.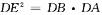 ;
;